오늘은 DISTANCE_MEASURE 함수에 관한 소개를 해볼까 합니다. 이 함수는 공간상에 여러 개의 데이터 포인트들이 흩어져있을 때 포인트와 포인트 사이의 거리를 측정하는 작업을 모든 쌍(pair)들에 대하여 수행하고 그 결과를 전달하는 역할을 합니다. 참고로 이러한 기능은 군집화(Clustering) 및 Dendrogram의 구성과 같은 작업의 기본이 됩니다(이와 관련해서는 차후에 기회가 되면 별도로 다룰 예정입니다). DISTANCE_MEASURE 함수의 사용에 있어서 공간의 차원에는 제한이 없습니다. 즉 1차원부터 N 차원까지 모두 적용 가능합니다. 그러면 오늘은 2차원 공간상에 분포하는 가상의 데이터 포인트들을 대상으로 하여 DISTANCE_MEASURE 함수를 적용하는 예제를 살펴보기로 하겠습니다. 먼저 가상의 데이터를 생성하는 과정은 다음과 같습니다.
data = [ $
[1, 1], $
[1, 3], $
[2, 2.2], $
[4, 1.75], $
[4, 4], $
[5, 1], $
[5.5, 3]]
HELP, data
sz = SIZE(data, /DIM)
n = sz[-1]
여기서는 2차원 공간상에 분포하는 7개의 포인트들을 가정하였습니다. 여기서 생성된 배열 data는 2x7의 구조를 갖는 2차원 배열인데 2는 차원의 갯수(여기서는 2차원)에 해당되고 7은 데이터 갯수에 해당됩니다. 데이터 갯수인 7은 별도로 추출하여 변수 n에 담았습니다. 이제 여기서 바로 DISTANCE_MEASURE 함수를 적용하면 됩니다.
distance = DISTANCE_MEASURE(data)
HELP, distance
이와 같이 DISTANCE_MEASURE 함수에 data를 바로 투입하면 됩니다. 기본적으로 이 함수에 투입될 데이터는 nxm의 형태를 갖는 2차원 배열이어야 한다는 것을 유의해야 합니다. 여기서 n은 차원의 갯수이고 m은 데이터 갯수입니다. 따라서 앞서 data를 2x7의 구조를 갖는 2차원 배열이 되도록 정의한 것도 이러한 이유입니다. 그리고 이 작업의 결과를 distance라는 항목으로 돌려받았는데, HELP에 의하여 출력된 내용을 보면 다음과 같습니다.
DISTANCE FLOAT = Array[21]
이와 같이 distance는 21개의 값들로 구성된 1차원 배열입니다. 하필 21개가 된 이유는 7개의 포인트들이 가질 수 있는 쌍(pair)들의 총 갯수가 21개이기 때문입니다. 비유를 하자면 7개의 팀들로 구성된 축구 리그가 있을 때 서로 한번씩 맞대결을 할 경우 필요한 총 경기수는 7*6/2=21이 되는 것과 동일한 개념입니다. 따라서 이러한 쌍들을 별도의 배열로 생성해두는 것도 필요한데, 그 과정은 다음과 같습니다.
i1 = !null
i2 = !null
FOR j = 0, n-2 DO BEGIN
FOR i = 1, n-1 DO BEGIN
IF i LE j THEN CONTINUE
i1 = [i1, j]
i2 = [i2, i]
ENDFOR
ENDFOR
이와 같은 작업을 수행하면 i1과 i2 각각 21개의 값들로 구성된 1차원 배열이 됩니다. 즉 앞서 얻은 distance와 동일한 구조입니다. 따라서 반복형 구문을 사용하여 다음과 같이 i1, i2, distance의 값들을 출력해볼 수 있습니다.
PRINT, 'Item# Item# Distance'
FOR j = 0, N_ELEMENTS(distance)-1 DO $
PRINT, i1[j], i2[j], distance[j], FORMAT='(I5, 1X, I5, 1X, F8.2)'
이 과정에 의하여 출력된 내용을 보면 다음과 같습니다.
Item# Item# Distance
0 1 2.00
0 2 1.56
0 3 3.09
0 4 4.24
0 5 4.00
0 6 4.92
1 2 1.28
1 3 3.25
1 4 3.16
1 5 4.47
1 6 4.50
2 3 2.05
2 4 2.69
2 5 3.23
2 6 3.59
3 4 2.25
3 5 1.25
3 6 1.95
4 5 3.16
4 6 1.80
5 6 2.06
이와 같이 각 쌍에 대하여 측정된 거리값을 목록화해서 볼 수 있습니다. 예를 들어 세번째 포인트(인덱스 2)와 여섯번째 포인트(인덱스 5) 사이의 거리는 3.23으로 측정되었음을 알 수 있습니다. 사실 DISTANCE_MEASURE 함수의 작업은 이러한 결과를 산출하는 것까지입니다. 다만 우리는 이러한 결과를 가시화하여 직관적으로 살펴보는 것도 필요할 것입니다. 따라서 이러한 작업을 계속 해봅시다. 먼저 2차원 공간상에 분포한 데이터 포인트들을 표출하는 작업은 SCATTERPLOT 함수를 사용하여 다음과 같이 처리해봅시다.
win = WINDOW(DIMENSIONS=[600, 500], /NO_TOOLBAR)
p = SCATTERPLOT(data[0, *], data[1, *], $
SYMBOL='circle', /SYM_FILLED, SYM_SIZE=2, SYM_COLOR='crimson', $
XRANGE=[0, 6], YRANGE=[0, 5], $
MARGIN=0.1, FONT_SIZE=10, /CURRENT)
표출 결과를 보면 다음과 같이 데이터 포인트들의 분포 형태를 알 수 있습니다.
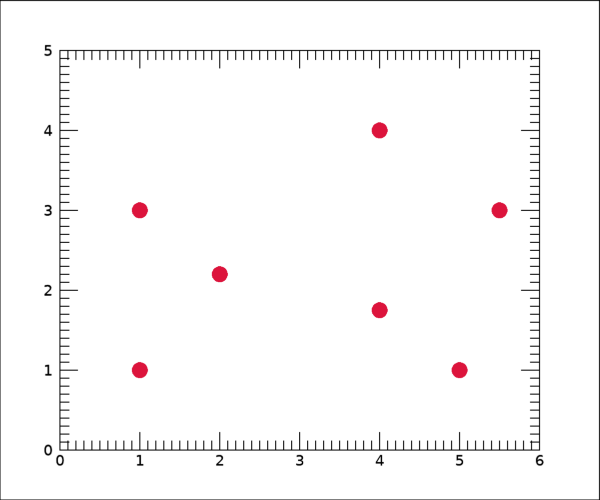
이제 앞서 DISTANCE_MEASURE 함수를 사용하여 얻은 결과를 이 그림 위에 중첩 표출해보고자 합니다. 먼저 모든 쌍들에 대하여 포인트 사이의 연결선을 표시하는 작업부터 해봅시다. 이러한 작업을 위해서는 어차피 반복형 구문의 사용이 필요합니다. 이 과정은 다음과 처리해봅시다.
FOR j = 0, N_ELEMENTS(distance)-1 DO BEGIN
px1 = data[0, i1[j]]
px2 = data[0, i2[j]]
py1 = data[1, i1[j]]
py2 = data[1, i2[j]]
line = POLYLINE([px1, px2], [py1, py2], COLOR='gray', /DATA)
ENDFOR
여기서는 각 쌍에 대하여 연결선을 이어야 할 두 포인트에 대한 X 좌표값들(px1, px2) 및 Y 좌표값들(py1, py2)을 추출하고 이들을 POLYLINE 함수에 투입하였습니다. 표출 결과를 보면 다음 그과 같습니다.

이와 같이 모든 쌍들에 대하여 총 21개의 연결선들이 그려진 것을 볼 수 있는데요. 여기에 추가로 각 쌍에 대하여 측정된 거리값도 함께 표시되면 더 좋을 것입니다. 거리값의 표시 위치는 각 쌍에 대한 연결선의 중간 부분이 적당하다고 보고 이러한 좌표를 계산하여 TEXT 함수에 반영되도록 하면 됩니다. 따라서 위의 반복형 구문의 내용을 다음과 같이 수정해봅시다.
FOR j = 0, N_ELEMENTS(distance)-1 DO BEGIN
px1 = data[0, i1[j]]
px2 = data[0, i2[j]]
py1 = data[1, i1[j]]
py2 = data[1, i2[j]]
line = POLYLINE([px1, px2], [py1, py2], COLOR='gray', /DATA)
tpx = 0.5*(px1+px2)
tpy = 0.5*(py1+py2)
tx = TEXT(tpx, tpy, STRING(distance[j], FORMAT='(F0.2)'), $
ALIGNMENT=0.5, FONT_COLOR='blue', FONT_SIZE=10, /DATA)
ENDFOR
여기서는 각 쌍에 대하여 거리값이 표시될 위치 좌표를 tpx, tpy로 얻고 이를 TEXT 함수에 투입하였습니다. 이러한 수정 사항이 반영된 표출 결과는 다음 그림과 같습니다.
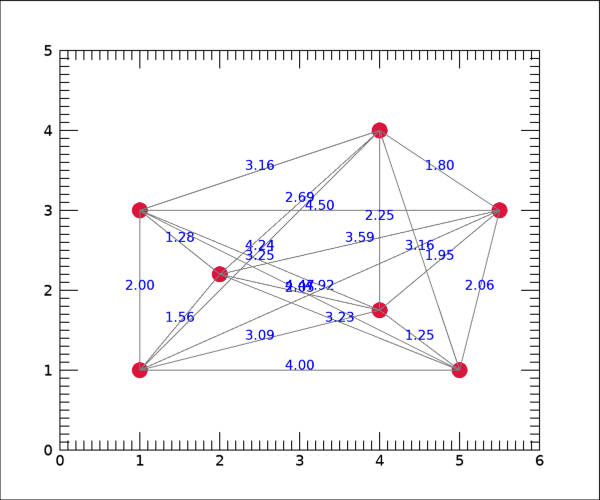
이 그림을 보면 각 쌍에 대한 연결선의 중간 부분에 거리값도 함께 표시된 것을 볼 수 있습니다. 이번에는 서로간의 거리가 가장 가까운 경우에 대해서만 연결선과 거리값이 표시되도록 해봅시다. 이를 위해서는 위의 반복형 구문의 내용에 다음과 같이 IF 구문을 하나 추가하면 될 것 같습니다.
FOR j = 0, N_ELEMENTS(distance)-1 DO BEGIN
IF distance[j] NE MIN(distance) THEN CONTINUE
px1 = data[0, i1[j]]
px2 = data[0, i2[j]]
py1 = data[1, i1[j]]
py2 = data[1, i2[j]]
line = POLYLINE([px1, px2], [py1, py2], COLOR='gray', /DATA)
tpx = 0.5*(px1+px2)
tpy = 0.5*(py1+py2)
tx = TEXT(tpx, tpy, STRING(distance[j], FORMAT='(F0.2)'), $
ALIGNMENT=0.5, FONT_COLOR='blue', FONT_SIZE=10, /DATA)
ENDFOR
결과는 다음 그림과 같습니다.
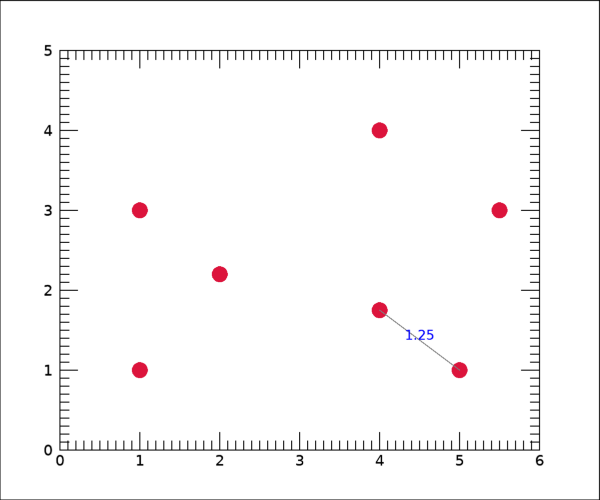
반대로 거리가 가장 먼 경우만 표시하고자 할 경우에는 위의 내용에서 IF 구문만 다음과 같이 수정하면 됩니다.
IF distance[j] NE MAX(distance) THEN CONTINUE
결과는 다음 그림과 같습니다.
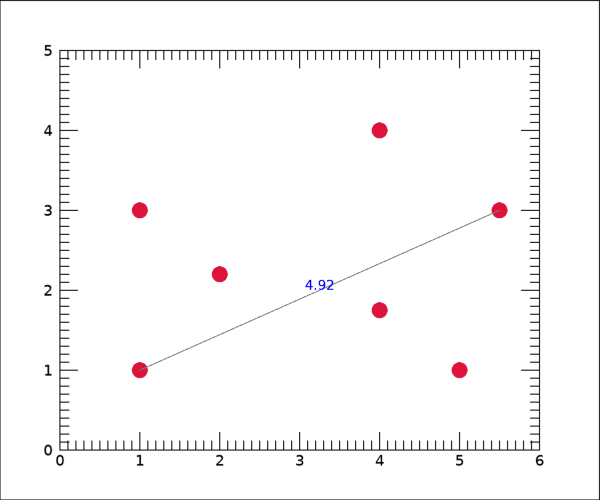
그리고 거리가 일정한 기준 이하인 경우들만 표시하고 싶은 경우 즉 예를 들어 거리가 2.0 이하인 경우들만 표시하고자 한다면 위의 내용에서 IF 구문을 다음과 같이 수정하면 됩니다.
IF distance[j] GT 2.0 THEN CONTINUE
결과는 다음 그림과 같습니다.

참고로 DISTANCE_MEASURE 함수의 MEASURE 및 POWER_MEASURE 키워드를 사용하면 거리를 계산하는 알고리즘을 따로 선택할 수도 있다는 것도 알아두면 좋을 것 같습니다. 어쨌든 이와 같이 공간상에 분포한 다수의 데이터 포인트들에 대하여 DISTANCE_MEASURE 함수를 적용하여 그 분석 결과를 이용하면, 서로 가깝게 몰려있는 포인트들을 하나의 군집으로 정의하는 것과 같은 작업(Clustering)이 가능합니다. 이와 관련된 내용은 차후에 이어서 다뤄보기로 하겠습니다.
'IDL > Math' 카테고리의 다른 글
| K-평균 군집화 분석 (K-means Clustering) (0) | 2023.10.25 |
|---|---|
| 군집화(Clustering)와 덴드로그램(Dendrogram) (1) | 2023.10.19 |
| Interpolation vs. Fitting (0) | 2021.08.02 |
| INTERPOL 함수를 이용한 1차원 내삽(1-d Interpolation) (0) | 2021.07.26 |
| MEDIAN 함수에 의한 중간값 산출에 관한 유의사항 (0) | 2021.06.18 |