공간상에 여러 개의 데이터 포인트들이 흩어져있을 때 포인트와 포인트 사이의 거리를 측정하는 작업을 모든 쌍(pair)들에 대하여 수행하고 그 결과를 전달하는 역할을 하는 DISTANCE_MEASURE 함수에 관하여 얼마전에 소개한 바 있습니다. 그리고 이러한 기능은 군집화(Clustering) 및 Dendrogram의 구축이라는 작업의 기본이 된다는 언급도 함께 하였습니다. 오늘은 바로 이어서 DISTANCE_MEASURE 함수로 얻은 결과를 바탕으로 군집화(Clustering) 작업을 수행하고 그 결과를 덴드로그램(Dendrogram)이라는 형태로 가시화하는 과정도 살펴보고자 합니다.
일단 분석에 사용되는 샘플 데이터는 지난회 게시물에서 생성했던 것을 그대로 사용하기로 합니다. 그러면 가상의 샘플 데이터를 생성하고 이들을 그림으로 표출하는 작업부터 먼저 시작해봅시다. 그 과정은 다음과 같습니다.
data = [ $
[1, 1], $
[1, 3], $
[2, 2.2], $
[4, 1.75], $
[4, 4], $
[5, 1], $
[5.5, 3]]
HELP, data
sz = SIZE(data, /DIM)
n = sz[-1]
win = WINDOW(DIMENSIONS=[600, 500], /NO_TOOLBAR)
p = SCATTERPLOT(data[0, *], data[1, *], $
SYMBOL='circle', /SYM_FILLED, SYM_SIZE=2, SYM_COLOR='crimson', $
XRANGE=[0, 6], YRANGE=[0, 5], $
MARGIN=0.1, FONT_SIZE=11, /CURRENT)
FOR j = 0, n-1 DO BEGIN
px = data[0, j]
py = data[1, j]
tx = TEXT(px, py-0.3, STRING(j, FORMAT='(I0)'), $
ALIGNMENT=0.5, FONT_COLOR='blue', FONT_SIZE=10, /DATA)
ENDFOR
이 내용은 지난회 게시물의 전반부에서 제시되었던 것과 거의 유사합니다. 다만 데이터 포인트들을 표시하면서 이번에는 이들의 일련 번호도 함께 표시하는 과정(진한색으로 표시된 반복형 구문)을 추가하여 약간의 수정을 해보았습니다. 일단 여기까지의 과정에 의하여 표출된 그림은 다음과 같습니다.

이와 같이 일련 번호들을 굳이 표시한 것은 나중에 얻게 될 군집화 분석의 결과를 알아보기 쉽게 하기 위함입니다. 그러면 지금부터 이 작업을 시작해봅시다. 먼저 다음과 같이 DISTANCE_MEASURE 함수를 사용하여 포인트들간의 거리 분석 결과부터 얻어야 합니다.
distance = DISTANCE_MEASURE(data)
HELP, distance
이 결과를 자세히 표시하고 가시화하는 과정은 지난회 게시물에서 이미 소개하였으므로 여기서는 생략하기로 합니다. 그대신 바로 이어서 군집화 분석 작업을 수행하기로 하겠습니다. 이를 위해서는 CLUSTER_TREE 함수를 사용하면 됩니다. 이 CLUSTER_TREE 함수는 계층적 군집 분석(Hierarchical Clustering)을 수행하는 역할을 합니다. 즉 공간상에 분포하는 다수의 데이터 포인트들에 대하여 거리가 가까운 것들을 군집(Cluster)으로 정의해나가는데, 작은 규모의 군집들을 먼저 정의하고 그 중에서도 서로 인접한 군집들을 모아서 상위의 군집으로 정의해나가는 식입니다. 이렇게 하위에서 상위까지 군집들을 정의해나가는 방식을 계층적 군집 분석이라고 하며 이러한 작업을 수행하는 역할을 바로 CLUSTER_TREE 함수가 수행한다고 보면 됩니다. 이 함수의 사용법 자체는 다음과 같이 매우 간단합니다.
clusters = CLUSTER_TREE(distance, linkdistance)
HELP, clusters, linkdistance
이와 같이 CLUSTER_TREE 함수에 대한 입력 데이터는 앞서 DISTANCE_MEASURE 함수로 얻었던 결과인 distance를 그대로 사용해야 합니다. 그러면 두 종류의 결과를 얻게 되는데요. 여기서는 clusters 및 linkdistance라는 두 배열로 결과를 얻었습니다. HELP에 의하여 출력된 내용을 보면 다음과 같습니다.
CLUSTERS LONG = Array[2, 6]
LINKDISTANCE FLOAT = Array[6]
각각 이와 같은 배열 구조를 하고 있는데요. 다음과 같이 반복형 구문을 사용하여 이 배열들의 실제 값을 출력해서 살펴봅시다.
PRINT, 'Item# Item# Distance'
FOR j = 0, N_ELEMENTS(linkdistance)-1 DO $
PRINT, clusters[0, j], clusters[1, j], linkdistance[j], $
FORMAT='(I5, 1X, I5, 1X, F8.2)'
실제로 출력된 내용을 보면 다음과 같습니다.
Item# Item# Distance
5 3 1.25
2 1 1.28
8 0 1.56
6 4 1.80
7 10 1.95
11 9 2.05
이제 이 내용이 구체적으로 어떤 의미인지를 살펴봐야 합니다. 먼저 데이터 포인트가 총 7개이며 일련번호는 0~6이라는 것을 다시 한번 상기합니다. 그리고 서로간의 거리가 가장 가까운 것부터 하나의 군집으로 간주되고 이러한 군집과 또 다른 인접한 포인트 또는 군집을 묶어서 또 상위의 군집으로 묶는 방식의 계층적 군집화 과정이 됩니다. 그래서 위의 내용에 대한 해석은 실제로는 다음과 같습니다.
1) 포인트 5와 포인트 3이 가장 먼저 하나의 군집으로 간주되며 이 군집에는 일련번호 7이 부여된다.
2) 포인트 2와 포인트 1이 하나의 군집으로 간주되며 이 군집에는 일련번호 8이 부여된다.
3) 군집 8과 포인트 0이 하나의 상위 군집으로 간주되며 이 군집에는 일련번호 9가 부여된다.
4) 포인트 6과 포인트 4가 하나의 군집으로 간주되며 이 군집에는 일련번호 10이 부여된다.
5) 군집 7과 군집 10이 하나의 상위 군집으로 간주되며 이 군집에는 일련번호 11이 부여된다.
6) 군집 11과 군집 9가 하나의 상위 군집으로 간주되는데 이것은 전체 포인트들에 해당된다.
이와 같이 원래의 데이터 포인트들은 일련번호 0~6이지만, 이후에 군집으로 간주되는 것들은 그 뒤의 일련번호들이 차례로 붙는 방식이 됩니다. 다만 아무래도 이러한 내용을 그냥 글로만 보기보다는 그림의 형태로 가시화하는 것이 필요할 것입니다. 그래서 이러한 군집들의 계층 구조를 도식화한 그림을 덴드로그램(Dendrogram)이라고 합니다. 물론 이러한 가시화도 가능한데 일단 이를 위해서는 DENDROGRAM 프로시저를 사용해야 합니다. 그 과정은 다음과 같습니다.
DENDROGRAM, clusters, linkdistance, outverts, outconn, $
LEAFNODES=leafnodes
HELP, leafnodes
PRINT, leafnodes
이와 같이 DENDROGRAM 프로시저에는 앞서 이미 얻은 clusters, linkdistance가 투입되어야 합니다. 그리고 여기서는 그 결과를 outverts, outconn 및 leafnodes라는 항목들로 돌려받았습니다. 일단 outverts와 outconn은 덴드로그램을 라인의 형태로 표시하는데 필요한 꼭지점 및 연결성 정보입니다. 그리고 leafnodes는 덴드로그램의 맨 아래 표시할 데이터 포인트 일련번호 숫자들이 됩니다. 그런데 DENDROGRAM 프로시저 자체는 그림을 표출하지는 않는다는 것을 유의해야 합니다. 다만 덴드로그램을 가시화하는데 필요한 정보들을 산출해줄 뿐입니다. 따라서 실제로 우리 눈으로 볼 수 있는 덴드로그램의 형태를 가시화하려면 별도의 과정이 필요합니다. 그 과정은 다음과 같이 구현해보았습니다.
wind = WINDOW(DIMENSIONS=[600, 500], /NO_TOOLBAR)
p = PLOT(outverts[0, *], outverts[1, *], $
SYMBOL='circle', /SYM_FILLED, SYM_SIZE=2, SYM_COLOR='crimson', $
XRANGE=[0, 6], YRANGE=[0, 2], /NODATA, AXIS_STYLE=0, $
MARGIN=0.1, /CURRENT)
dg = POLYLINE(REFORM(outverts[0, *]), REFORM(outverts[1, *]), $
CONNECTIVITY=outconn, COLOR='blue', THICK=2, CLIP=0, /DATA)
txloc = FINDGEN(N_ELEMENTS(leafnodes))
FOR j = 0, N_ELEMENTS(leafnodes)-1 DO $
dtx = TEXT(txloc[j], -0.1, STRING(leafnodes[j], FORMAT='(I0)'), $
ALIGNMENT=0.5, FONT_SIZE=11, COLOR='crimson', CLIP=0, /DATA)
tx = TEXT(0.5, 0.95, 'Dendrogram', FONT_SIZE=14, ALIGNMENT=0.5, /NORMAL)
이와 같이 별도의 그래픽창을 띄우고, 앞서 DENDROGRAM 프로시저를 실행하여 얻은 결과 항목들을 PLOT, POLYLINE, TEXT 함수들에 투입하여 실제로 눈에 보이는 덴드로그램의 형태로 표출하는 과정이 필요합니다. 표출 결과는 다음 그림과 같습니다.
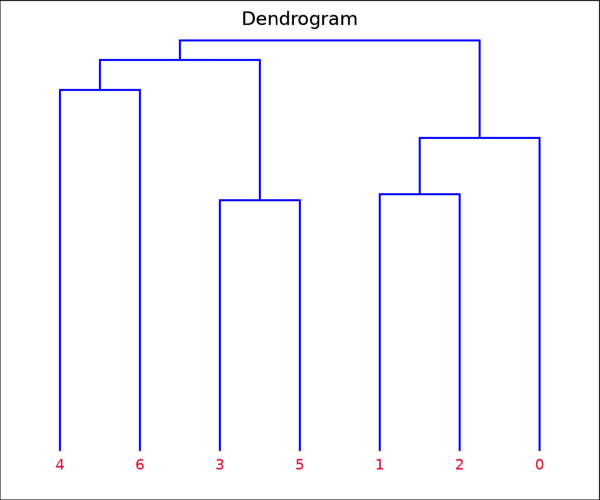
이와 같이 앞서 군집화 분석의 결과를 글로 기술했던 내용을 덴드로그램이라는 형태로 가시화한 모습이라고 보면 됩니다. 물론 이 그림에서도 데이터 포인트들은 일련번호로만 표시된 상태이기 때문에, 앞서 데이터 포인트들을 직접 표시했던 그림과 함께 보는 것이 좋습니다. 어쨌든 다수의 데이터 포인트들이 분포하는 상태에서 거리 기반으로 포인트들에 대하여 계층적 군집화를 수행하고 그 결과를 조회 및 가시화하는 예제를 살펴보았습니다. 이 과정에서는 DISTANCE_MEASURE, CLUSTER_TREE, DENDROGRAM 등과 같은 주요 관련 기능들을 사용하면 됩니다. 그리고 예제에서는 7개의 포인트들로 구성된 예제 데이터를 사용하였는데요. 만약 훨씬 더 많은 포인트들로 구성된 데이터일 경우라면 그 결과도 좀 더 복잡해지긴 할 것입니다.
군집화와 덴드로그램에 관한 내용은 일단 이 정도로 마무리합니다. 그리고 IDL에서는 계층적 군집 분석 외에도 K-Means라는 알고리즘을 기반으로 한 군집화 기능도 제공됩니다. 이와 관련된 내용은 추후에 따로 정리하여 소개해보기로 하겠습니다.
'IDL > Math' 카테고리의 다른 글
| 증가 및 감소 연산자 (Increment and Decrement Operator) (1) | 2023.11.20 |
|---|---|
| K-평균 군집화 분석 (K-means Clustering) (0) | 2023.10.25 |
| DISTANCE_MEASURE 함수 소개 (0) | 2023.10.12 |
| Interpolation vs. Fitting (0) | 2021.08.02 |
| INTERPOL 함수를 이용한 1차원 내삽(1-d Interpolation) (0) | 2021.07.26 |