IDL에서 군집화 분석 작업을 하는 방법에 관하여 얼마전에 관련 게시물을 통하여 소개한 바 있습니다. 여기서는 계층적 군집 분석(Hierachical Clustering) 알고리즘을 기반으로 군집화를 수행하는 방법을 설명하였고, 이러한 작업을 위하여 DISTANCE_MEASURE, CLUSTER_TREE, DENDROGRAM 등의 기능들을 사용하는 방법 및 관련 예제들을 소개하였습니다. 그런데 IDL에서는 군집화 분석에 있어서 이러한 계층적 분석 기법 외에도 또 다른 기법을 사용할 수도 있습니다. 바로 K-평균 알고리즘을 바탕으로 하는 K-평균 군집화(K-means Clustering) 분석 기법입니다. 이 알고리즘은 웹상에서 검색을 해보면 "주어진 데이터를 k개의 클러스터로 묶는 알고리즘으로, 각 클러스터와 거리 차이의 분산을 최소화하는 방식"이라고 소개되어 있습니다. 여기서는 이 알고리즘 자체에 대한 원론적인 접근은 배제하고, IDL에서 관련 기능들을 사용하여 결과를 얻는 과정을 소개하는 것에 촛점을 맞추도록 하겠습니다.
일단 예제 데이터는 얼마전 계층적 군집 분석에 관한 소개를 할 때 사용했던 데이터를 그대로 사용하도록 하겠습니다. 이러한 가상 데이터를 생성하고 기본적인 표출까지 하는 과정은 다음과 같습니다.
data = [ $
[1, 1], $
[1, 3], $
[2, 2.2], $
[4, 1.75], $
[4, 4], $
[5, 1], $
[5.5, 3]]
HELP, data
win = WINDOW(DIMENSIONS=[600, 500], /NO_TOOLBAR)
p = SCATTERPLOT(data[0, *], data[1, *], $
SYMBOL='circle', SYM_SIZE=2, /SYM_FILLED, $
XRANGE=[0, 6], YRANGE=[0, 5], $
MARGIN=0.1, FONT_SIZE=11, /CURRENT)
여기까지의 과정에 의하여 표출된 모습은 다음과 같습니다.

이제 이 데이터에 대하여 K-평균 군집화 알고리즘을 적용해봅시다. 이를 위해서는 CLUST_WTS 및 CLUSTER 함수를 차례로 사용하면 됩니다. 먼저 CLUST_WTS 함수는 주어진 데이터를 여러 군집들로 나누는데 있어서 각 군집의 중심이 될 위치를 가중치(Weight)의 개념으로 산출하는 역할을 합니다. 이 작업은 먼저 k개의 초기 군집들을 임의로 설정한 다음 각 군집 내에서 포인트들간의 거리 차이의 분산은 최소화하고 군집간의 거리 차이의 분산은 최대화하는 방식으로 반복작업(iteration)을 계속 수행하여 최종적인 결과를 얻는 방식으로 진행됩니다. CLUST_WTS 함수는 다음과 같이 사용해봅시다.
weights = CLUST_WTS(data, N_CLUSTERS=2)
HELP, weights
PRINT, weights
기본적으로 CLUST_WTS 함수에 투입되는 데이터는 nxm의 구조를 갖는 2차원 배열이어야 합니다. 여기서 투입된 배열 data는 2x7의 구조를 갖는데, 2는 변수들의 갯수로서 각각 X 좌표값들 및 Y 좌표값들에 해당되고 7은 데이터 포인트들의 총 갯수에 해당됩니다. 그리고 N_CLUSTERS 키워드를 사용하면서 2라는 값을 부여하였는데요. 이 키워드는 말 그대로 주어진 데이터 포인트들을 총 몇 개의 군집들로 나눌 것인가를 미리 설정하는 역할을 합니다. 사실 이 키워드의 사용은 필수는 아닙니다. 다만 사용하지 않을 경우에는 군집의 갯수를 CLUST_WTS 함수가 알아서 결정하게 되는데, 이렇게 할 경우에는 결과의 일관성 및 타당성이 떨어질 수도 있다는 단점이 있습니다. 이러한 단점은 데이터 포인트들의 군집 구분이 뚜렷하지 않고 모호한 경우일수록 더 두드러지게 나타납니다. 따라서 가급적이면 군집의 갯수를 사전에 설정해두는 것을 권장합니다. 어쨌든 이 결과로 얻어진 weights라는 배열에 관한 정보 및 그 값들이 출력된 내용을 보면 다음과 같습니다.
WEIGHTS FLOAT = Array[2, 2]
4.73310 2.45180
1.39025 2.12846
이것은 2개의 군집 각각의 중심위치에 해당됩니다. 즉 애초에 CLUST_WTS 함수를 사용할 때 군집 갯수를 2개로 설정해두었기 때문에 이 함수가 얻은 결과에 의하여 각 군집의 중심 위치에 대한 좌표값들이 계산된 것입니다. 이 결과에 의하면 군집 1의 위치좌표는 대략 (4.73, 2.45)이고 군집 2의 위치좌표는 대략 (1.39, 2.13)인 것으로 파악되었습니다. 그러면 이 위치들을 그림상에 중첩하여 표시해봅시다. 이를 위해서는 다음과 같이 SCATTERPLOT 함수를 활용하면 됩니다.
pw = SCATTERPLOT(weights[0, *], weights[1, *], $
SYMBOL='circle', SYM_SIZE=2, /SYM_FILLED, SYM_COLOR='red', /OVERPLOT)
표출 결과는 다음 그림과 같습니다.

여기서 빨간 점으로 표시된 부분이 바로 각 군집의 중심 위치가 됩니다. 실제로 데이터 포인트들의 분포를 보면 좌측 군집과 우측 군집으로 대략 나눌 수 있다는 것을 육안으로도 짐작할 수 있는데요. 수치적인 분석 결과도 크게 다르지 않다는 것을 확인할 수 있습니다. 이제 다음 단계는 CLUSTER 함수를 사용하여 군집 분석 결과를 최종적으로 산출하는 과정입니다. 그 과정은 다음과 같습니다.
result = CLUSTER(data, weights, N_CLUSTERS=2)
HELP, result
PRINT, result
이와 같이 CLUSTER 함수에는 대상 데이터 배열인 data 그리고 좀전에 CLUST_WTS 함수에 의하여 얻은 결과인 weights가 투입됩니다. 그리고 N_CLUSTERS 키워드의 값을 똑같이 2로 설정해주어야 합니다. 그리고 이 결과를 result라는 항목으로 얻었는데 이 항목에 대하여 HELP, PRINT에 의하여 출력된 내용을 보면 다음과 같습니다.
RESULT LONG = Array[1, 7]
1
1
1
0
0
0
0
이것은 각 데이터 포인트가 소속된 군집의 일련번호를 인덱스로 나타내는 것입니다. 즉 첫번째 군집(인덱스는 0)의 구성 멤버들은 데이터 포인트 3, 4, 5, 6이고 두번째 군집(인덱스는 1)의 구성 멤버들은 데이터 포인트 0, 1, 2가 된다는 의미입니다. 그러면 이 결과를 이용하여 그림상에서 각 군집이 서로 구분되도록 표출해봅시다. 이를 위해서는 앞서 weights를 활용하여 각 군집의 중심 위치를 표시했던 과정의 뒷부분에 다음과 같이 results를 활용하여 각 군집을 서로 다른 색상으로 표시하는 과정을 추가하면 됩니다.
p1 = SCATTERPLOT(data[0, WHERE(result EQ 0)], data[1, WHERE(result EQ 0)], $
SYMBOL='circle', SYM_SIZE=2, /SYM_FILLED, SYM_FILL_COLOR='cyan', $
SYM_COLOR='black', /OVERPLOT)
p2 = SCATTERPLOT(data[0, WHERE(result EQ 1)], data[1, WHERE(result EQ 1)], $
SYMBOL='circle', SYM_SIZE=2, /SYM_FILLED, SYM_FILL_COLOR='gold', $
SYM_COLOR='black', /OVERPLOT)
이렇게 하면 첫번째 군집에 속하는 데이터 포인트들은 cyan 색상으로 그리고 두번째 군집은 gold 색상으로 표시될 것입니다. 표출 결과는 다음 그림과 같습니다.

결국 이 그림은 7개의 모든 데이터 포인트들을 두 개의 군집으로 나누어서 각 군집에 속하는 데이터 포인트들을 서로 다른 색상으로 표시하고 또한 각 군집의 중심 위치도 함께 한 결과가 됩니다. 사실 이 데이터의 경우는 포인트들의 갯수도 적고 육안으로 봐도 대략 어떤 식으로 군집을 나눌 수 있을 것인가가 잘 보이는 편이긴 합니다. 그러면 데이터 포인트들의 갯수가 훨씬 더 많은 경우에는 어떨까요? 이러한 경우를 테스트해보기 위하여 샘플 데이터를 변경해봅시다. 이를 위하여 맨 처음에 data 배열을 정의했던 부분만 다음과 같은 내용으로 변경해봅시다.
n = 50
x1 = RANDOMN(seed, n)/1.7+1.8
y1 = RANDOMN(seed, n)/1.9+3.1
x2 = RANDOMN(seed, n)/2.1+4.4
y2 = RANDOMN(seed, n)/1.8+2.6
data = TRANSPOSE([[x1, x2], [y1, y2]])
HELP, data
이와 같이 하면 배열 data가 이번에는 2x100의 형태를 갖게 됩니다. 즉 100개의 포인트들로 구성된 샘플 데이터가 생성됩니다. 나머지 과정은 동일합니다. 최종 결과만 그림으로 보면 다음과 같습니다.
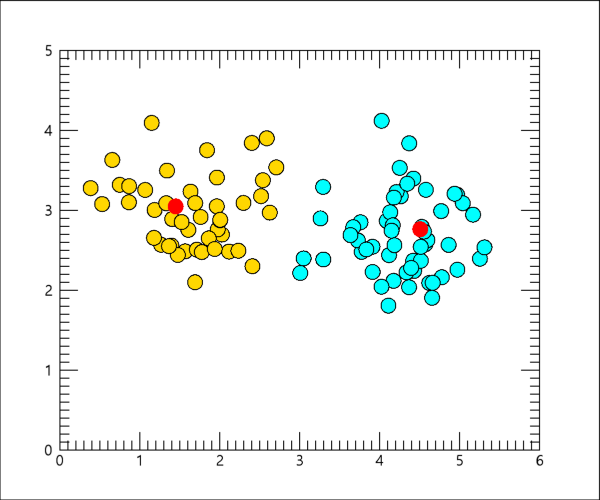
여기서는 샘플 데이터를 난수 기반으로 생성하기 때문에 실행할 때마다 그 모습은 달라집니다. 따라서 여러분의 결과도 이 그림과는 약간 다를 것이지만, 전반적인 맥락은 유사할 것입니다.
어쨌든 K-means Clustering 알고리즘을 적용하여 데이터 포인트들을 군집화하기 위해서는 CLUST_WTS 및 CLUSTER 함수를 이와 같이 활용하면 됩니다. 그리고 예제에서는 2차원 공간내에 분포한 데이터를 대상으로 하였지만, 데이터의 차원에는 제한이 없습니다. 따라서 3차원 공간내에 분포한 데이터를 대상으로도 얼마든지 적용 가능합니다. 그리고 이전 게시물에서 소개했던 계층적 군집화(Hierarchical Clustering) 기법도 있다는 점을 함께 참조하면 좋을 것 같습니다.
'IDL > Math' 카테고리의 다른 글
| VALUE_LOCATE 함수 소개 (0) | 2024.06.07 |
|---|---|
| 증가 및 감소 연산자 (Increment and Decrement Operator) (1) | 2023.11.20 |
| 군집화(Clustering)와 덴드로그램(Dendrogram) (1) | 2023.10.19 |
| DISTANCE_MEASURE 함수 소개 (0) | 2023.10.12 |
| Interpolation vs. Fitting (0) | 2021.08.02 |