제가 이 블로그를 통해서 내삽 또는 보간(Interpolation)이라는 기법과 근사(Fitting)라는 기법을 IDL에서 사용하는 방법에 관하여 관련 내장함수들에 대한 소개 및 예제들을 여러 차례에 걸쳐 소개해드린 바 있습니다. 오늘은 이와 관련하여 조금은 원론적인 얘기를 해보고자 하는데요. 바로 내삽(Interpolation)과 근사(Fitting)의 차이점에 관한 것입니다. 사실 이 두가지 기법은 서로 비슷한 것처럼 느껴질 수도 있습니다. 물론 제가 수치계산 분야의 전문가는 아니기 때문에 학문적으로 완벽한 지식을 갖고 얘기할 수 있는 입장이 아니긴 하지만, 적어도 IDL에서 지원되는 관련 기능들의 관점에서 본다면 두 기법은 서로 완전히 다르다고 얘기할 수 있습니다. 예제 데이터 및 처리 결과를 보면서 살펴보기로 하겠습니다.
먼저 예제 데이터는 다음과 같이 생성합니다.
n = 21
x = FINDGEN(n)*0.5
y = x*0.6+5+RANDOMU(-1, n)*3
이와 같이 x는 0~10의 범위 내에서 0.5의 간격으로 21개의 값들로 구성되고, y는 RANDOMU 함수를 사용하여 대략 5~15의 범위 내에 존재하는 난수값들로 생성하였습니다. 이렇게 생성된 x, y 데이터를 다음과 같이 표출해봅시다.
win = WINDOW(DIMENSIONS=[800, 600], /NO_TOOLBAR)
p = PLOT(x, y, SYMBOL='circle', /SYM_FILLED, SYM_COLOR='blue', $
YRANGE=[5, 15], LINESTYLE=6, XTITLE='X', YTITLE='Y', $
FONT_SIZE=11, MARGIN=0.1, /CURRENT, CLIP=0)
표출된 모습은 다음 그림과 같습니다.

먼저 내삽에 의한 처리 결과부터 산출해보겠습니다. 다음과 같이 INTERPOL 함수를 사용하여 선형 내삽(Linear Interpolation) 결과를 얻고, 앞선 표출 그림에 중첩하여 표출합니다.
xf = x
yf = INTERPOL(y, x, xf)
pf = PLOT(xf, yf, COLOR='crimson', THICK=2, /OVERPLOT)
선형 내삽에 의하여 얻어진 결과가 원본 데이터와 함께 중첩된 모습은 다음 그림과 같습니다.

참고로 INTERPOL 함수를 사용하여 선형 내삽 결과를 얻는 방법에 관한 자세한 내용에 대해서는 아래 링크의 관련 게시물을 참조하시기 바랍니다.
https://blog.daum.net/swrush/604
일단 선형 내삽에 의한 결과는 얻었습니다. 그러면 이번에는 선형 근사(Linear Fitting)에 의한 결과를 얻어보겠습니다. 이를 위해서는 다음과 같이 LINFIT 함수를 사용하여 근사 결과를 얻고, 앞서 처음에 표출했던 원본 데이터 표출 그림상에 중첩하여 표출합니다.
err = MAKE_ARRAY(n, VALUE=1.0)
coeff = LINFIT(x, y, YFIT=yfit, CHISQR=csq, $
PROB=prb, MEASURE_ERROR=err)
plo = PLOT(x, yfit, COLOR='crimson', THICK=2, /OVERPLOT)
선형 내삽의 결과와 원본 데이터가 중첩 표출된 모습은 다음 그림과 같습니다.

참고로 LINFIT 함수를 사용하여 선형 근사 결과를 얻는 방법에 관한 자세한 내용에 대해서는 아래 링크의 관련 게시물을 참조하시기 바랍니다.
https://blog.daum.net/swrush/500
어쨌든 이와 같이 선형 내삽에 의한 결과 및 선형 근사에 의한 결과를 모두 얻고 표출까지 해보았습니다. 두 결과를 비교해보면 두 기법 사이의 차이점이 극명하게 드러납니다. 선형 내삽에 의한 결과를 보면 모든 데이터 포인트들이 빠짐없이 직선으로 이어져 있습니다. 반면 선형 근사에 의한 결과를 보면 데이터 포인트들을 모두 이어주는게 아니고 전반적인 경향에 가장 잘 부합되는 직선의 식을 얻은 것입니다. "가장 잘 부합되는" 직선을 찾는데 있어서는 최소자승법(Least Square)이 적용됩니다. 두 결과를 나란히 비교해보면 다음 그림과 같습니다.
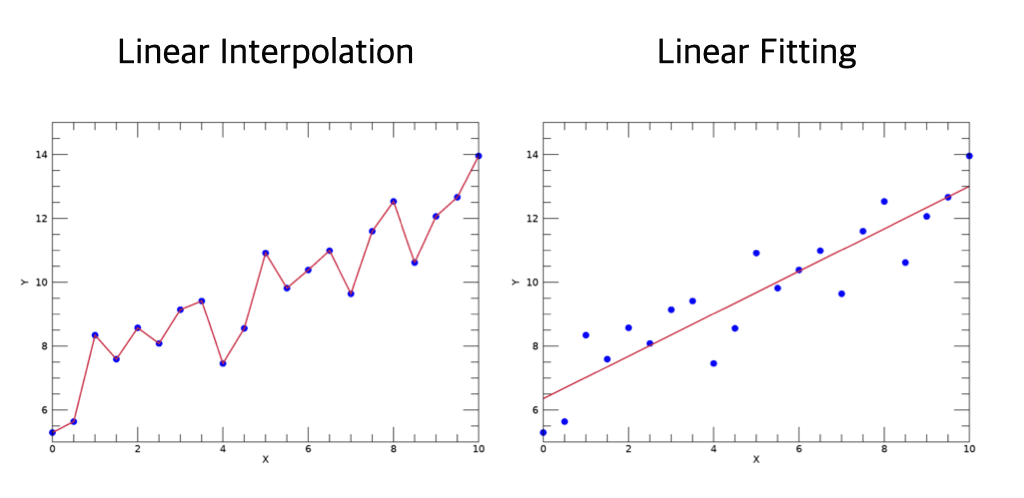
결국 내삽(Interpolation)이라는 기법은 데이터 포인트들을 어떻게든 모두 이어주는 결과를 얻는 것이고, 근사(Fitting)라는 기법은 데이터 포인트들을 무조건 이어주기보다는 전반적인 경향을 가장 잘 맞추는 결과를 얻는 것이라는 차이점이 있다고 보면 됩니다. 물론 내삽과 근사 중 어떤 기법이 더 적합하느냐는 데이터의 특성이나 처리의 목적 등에 따라 연구자의 판단에 의하여 결정될 문제라는 점을 반드시 유념해야 합니다.
'IDL > Math' 카테고리의 다른 글
| 군집화(Clustering)와 덴드로그램(Dendrogram) (1) | 2023.10.19 |
|---|---|
| DISTANCE_MEASURE 함수 소개 (0) | 2023.10.12 |
| INTERPOL 함수를 이용한 1차원 내삽(1-d Interpolation) (0) | 2021.07.26 |
| MEDIAN 함수에 의한 중간값 산출에 관한 유의사항 (0) | 2021.06.18 |
| GAUSS2DFIT 함수를 이용한 2차원 Gaussian 함수 근사 (0) | 2021.01.05 |