감마 보정(Gamma Correction)은 이미지 처리 분야에서 널리 사용되고 있는 기법으로서 비선형적인 전달 함수(Nonlinear Transfer Function)를 사용하여 신호의 강도를 변형시키는 작업을 의미합니다. 이 기법에서 사용되는 비선형 전달 함수의 형태는 다음과 같습니다. 이 식에서 지수 형태로 들어가는 gamma 값이 가장 핵심적인 역할을 합니다.
f(x) = gain*x^gamma+offset
물론 IDL에서도 이러한 기법을 사용하는 것이 가능합니다. 어떻게 보면 여기서 예전에 소개되었던 클리핑(Clipping) 기법 또는 히스토그램 균일화(Histogram Equalization) 기법과 유사한 맥락일 수도 있지만, 감마 보정 기법의 경우는 전달 함수의 형태를 다양하게 변형시켜서 적용할 수 있다는 차별적인 특성이 있습니다. 그래서 IDL에서 이미지 데이터에 대하여 감마 보정 기법을 적용하는 방법 및 예제를 이번 기회에 살펴보고자 합니다.
먼저 예제로 사용할 가상의 2차원 데이터를 다음과 같이 정의해봅시다.
x = [0:6:0.01]
y = [0:4:0.01]
xx = x#(FLTARR(N_ELEMENTS(y))+1)
yy = y##(FLTARR(N_ELEMENTS(x))+1)
data = (1+SIN(yy*5))*xx^2
HELP, xx, yy, data
PRINT, MIN(data), MAX(data)
여기서 정의된 data는 601x401의 구조를 갖는 2차원 배열이며 값 범위는 0~72가 됩니다. 그리고 x는 X축 방향의 601개의 격자값들로 구성된 1차원 배열이고 y는 Y축 방향의 401개의 격자값들로 구성된 1차원 배열이 됩니다. 그런데 xx의 경우는 X축 방향으로 증가하는 601개의 격자값들이 2차원적으로 분포하도록 인위적으로 재구성된 601x401 구조의 배열이 됩니다. 또한 yy의 경우는 Y축 방향으로 증가하는 401개의 격자값들이 2차원적으로 분포하도록 인위적으로 재구성된 601x401 구조의 배열이 됩니다. 배열 xx를 구성하는 값들의 구조를 대략적으로 본다면 다음과 같습니다.
0.01 0.02 0.03 0.04 0.05 ~~~~~ 0.58 0.59 0.60
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
0.01 0.02 0.03 0.04 0.05 ~~~~~ 0.58 0.59 0.60
0.01 0.02 0.03 0.04 0.05 ~~~~~ 0.58 0.59 0.60
0.01 0.02 0.03 0.04 0.05 ~~~~~ 0.58 0.59 0.60
그리고 배열 yy를 구성하는 값들의 구조를 대략적으로 본다면 다음과 같습니다.
0.60 0.60 0.60 ~~~~~ 0.60 0.60
0.59 0.59 0.59 ~~~~~ 0.59 0.59
~~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~~
0.03 0.03 0.03 ~~~~~ 0.03 0.03
0.02 0.02 0.02 ~~~~~ 0.02 0.02
0.01 0.01 0.01 ~~~~~ 0.01 0.01
이와 같이 1차원 배열인 x, y로부터 2차원 배열인 xx, yy를 굳이 또 재구성한 이유는 data라는 2차원 배열의 값들을 산출하는 수식(1+SIN(yy*5))*xx^2)에 투입하기 위해서라고 보면 됩니다. HELP에 의하여 출력된 내용을 보면 다음과 같습니다.
XX FLOAT = Array[601, 401]
YY FLOAT = Array[601, 401]
DATA FLOAT = Array[601, 401]
0.00000 71.9997
이제 그래픽 창을 띄우고 이 데이터를 이미지로 표출해봅시다. 여기서는 가로 방향으로 길쭉한 그래픽 창을 띄워서 방금 정의된 2차원 배열에 대한 이미지를 왼쪽에 띄웁니다. 오른쪽 공간에는 나중에 감마 보정을 적용한 결과 이미지를 띄울 예정입니다. 그래픽 창의 생성 및 이미지 표출까지의 과정은 다음과 같습니다.
ct = COLORTABLE(0)
win = WINDOW(DIMENSIONS=[1200, 500], /NO_TOOLBAR)
i1 = IMAGE(data, xx, yy, RGB_TABLE=ct, ASPECT_RATIO=0, $
XMINOR=0, YMINOR=0, XTICKLEN=0, YTICKLEN=0, $
POSITION=[0.05, 0.2, 0.45, 0.92], TITLE='Original', $
AXIS_STYLE=2, /CURRENT)
cb1 = COLORBAR(POSITION=[0.1, 0.05, 0.4, 0.09], /BORDER, $
RANGE=[MIN(data), MAX(data)], MINOR=0, TICKINTERVAL=10)
여기서는 흑백 계열 색상으로 구성된 디폴트 컬러테이블을 사용하여 이미지를 표출하고 하단에 컬러바까지 표시하였습니다. 일단 여기까지의 내용을 실행하면 표출 결과는 다음 그림과 같습니다.
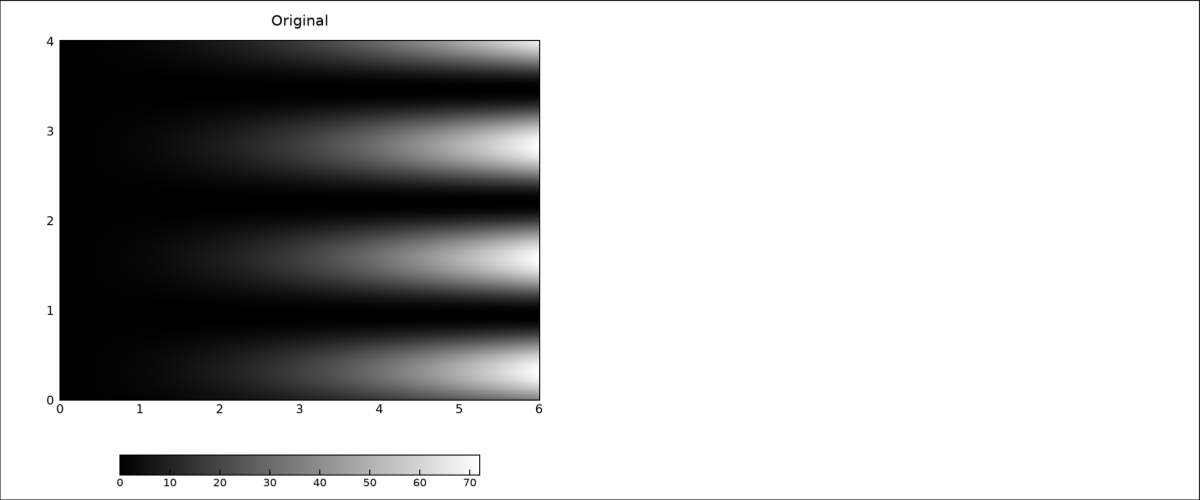
그러면 이제 감마 보정을 할 차례입니다. 원래 IDL에서는 감마 보정 기능을 담당하는 GAMMA_CT 명령이 지원됩니다. 따라서 이 명령을 사용하는 것이 기본이긴 합니다. 다만 이 명령 자체가 옛날 옛적에 IDL의 그래픽 체계가 DG(Direct Graphics)만 존재했던 시기에 만들어졌고 그 동작 방식도 DG 체계 기준으로만 국한되어 있습니다. 게다가 제가 사용해본 바로는 사용 방법 및 결과 산출의 방식도 지금 기준에서는 다소 불편한 측면이 있다고 생각이 됩니다. 그래서 기본적인 틀은 유지하면서 제 나름대로 DG 체계 뿐 아니라 NG 체계에서도 비교적 쉽게 사용할 수 있는 버전을 따로 만들어보았습니다. 편의상 그 명칭을 GAMMA_CT_SWLEE라고 하였고 그 파일은 아래에 첨부합니다.
따라서 이후의 작업에서는 위에 첨부한 GAMMA_CT_SWLEE 명령을 사용하여 감마 보정 작업을 수행하기로 합니다. 일단 이 명령은 이미지 데이터 자체에 대하여 보정을 하는 것이 아니고 이미지의 표출에 사용되는 컬러테이블에 대하여 감마 보정 기법 기반의 변형을 가하는 방식으로 작동한다는 것을 미리 염두에 둘 필요가 있습니다. 따라서 이렇게 변형된 컬러테이블을 사용하여 이미지 데이터를 다시 표출하면 감마 보정이 적용된 이미지를 얻게 되는 방식입니다. 이 명령을 사용하는 문법은 다음과 같습니다.
GAMMA_CT_SWLEE, gm, ct
여기서 gm은 감마 보정에 적용되는 전달 함수의 지수에 해당되는 감마(Gamma) 값인데 이 값이 1이면 선형이 되고 1보다 크거나 작은 값이 되면 본격적인 변형이 발생하게 됩니다. 즉 gm의 값이 1이면 감마 보정을 안하는 것과 마찬가지가 되므로 큰 의미가 없고, 1보다 크거나 작은 값을 투입해야 의미가 있다고 보면 됩니다. 그리고 ct는 컬러테이블을 구성하는 색상들의 RGB 값들로 구성된 256x3의 구조를 갖는 배열이 되어야 합니다. 즉 현재 사용중인 컬러테이블에 대한 RGB 데이터 배열인 ct를 gm과 함께 이 명령에 투입하면, 감마 보정을 거쳐 변형된 RGB 데이터인 새로운 ct가 유저에게 전달되는 방식입니다. 따라서 GAMMA_CT_SWLEE 명령에 투입되는 ct와 명령이 실행된 이후에 얻어지는 ct는 서로 다르다는 점을 반드시 유의해야 합니다. 그러면 gm의 값을 0.5로 정의하고 ct는 앞서 이미 정의했던 것을 그대로 사용하여 다음과 같이 진행해봅시다.
gm = 0.5
GAMMA_CT_SWLEE, gm, ct
위의 내용이 실행되면 변형된 ct를 얻게 되므로 이러한 ct를 이용하여 이미지 데이터를 표출하면 됩니다. 이러한 이미지는 앞서 생성했던 그래픽 창의 오른쪽에 표시되도록 합시다. 이러한 작업을 위하여 다음과 같은 과정을 추가합니다.
i2 = IMAGE(data, xx, yy, RGB_TABLE=ct, ASPECT_RATIO=0, $
XMINOR=0, YMINOR=0, XTICKLEN=0, YTICKLEN=0, $
POSITION=[0.55, 0.2, 0.95, 0.92], AXIS_STYLE=2, $
TITLE='Gamma Corrected with '+STRING(gm, FORMAT='(F0.1)'), $
/CURRENT)
cb2 = COLORBAR(TARGET=i2, POSITION=[0.6, 0.05, 0.9, 0.09], /BORDER, $
RANGE=[MIN(data), MAX(data)], MINOR=0, TICKINTERVAL=10)
이러한 내용까지 모두 실행하면 그 결과는 다음 그림과 같습니다.

이 그림에서 왼쪽과 오른쪽을 서로 비교해보면 감마 보정의 효과가 어떤 것인지 가늠해볼 수 있습니다. 이미지 자체의 모습도 서로 다를 뿐 아니라 하단의 컬러바 역시 서로 다릅니다. 이와 같이 감마의 값이 0.5인 경우에는 컬러바 기준으로 어두운 부분 즉 검정색~짙은 회색 계열인 부분이 축소되는 반면 밝은 부분 즉 옅은 회색~흰색 계열 색상의 점유율이 더 커집니다. 그러한 특성이 이미지에서도 그대로 반영된 것을 볼 수 있습니다. 즉 감마의 값이 1보다 작으면 이와 비슷한 방식으로 이미지가 변형되는데, 이것은 결국 원본 이미지에서 화소값이 낮았던 부분들의 명암이 더 강조되고 가독성이 높아지는 효과로 나타나게 됩니다. 이것은 원본 이미지에서 그 값이 낮았던 화소들 중 상당수가 더 높은 화소값들로 대체됨으로써, 전반적으로 화소값도 높아지면서도 명암 대비는 더 커지기 때문입니다. 이와 같은 감마 보정에 의하여 컬러테이블이 변형된 방식에 대한 이해를 돕기 위한 도식적인 그림을 보면 다음과 같습니다.

그러면 반대로 감마의 값을 1보다 크게 하면 어떻게 될까요? 위의 내용에서 변수 gm의 값만 2.5로 변경하여 전체 과정을 다시 실행해보면 그 결과는 다음 그림과 같습니다.

이 그림을 보면 감마의 값이 1보다 클 경우에 얻게 되는 감마 보정 효과가 어떤 것인지를 가늠해볼 수 있습니다. 즉 이와 같이 감마의 값이 2.5인 경우에는 컬러바 기준으로 밝은 부분 즉 옅은 회색~흰색 계열인 부분이 축소되는 반면 어두운 부분 즉 검정색~짙은 회색 계열 색상의 점유율이 더 커집니다. 이것은 결국 원본 이미지에서 화소값이 높았던 부분들의 명암이 더 강조되고 가독성이 높아지는 효과로 나타나게 됩니다. 이것은 원본 이미지에서 그 값이 높았던 화소들 중 상당수가 더 낮은 화소값들로 대체됨으로써, 전반적으로 화소값도 낮아지면서도 명암 대비는 더 커지기 때문입니다. 이와 같은 감마 보정에 의하여 컬러테이블이 변형된 방식에 대한 이해를 돕기 위한 도식적인 그림을 보면 다음과 같습니다.

오늘은 이와 같이 이미지 데이터에 대하여 감마 보정을 적용하는 기본적인 방법을 예제와 함께 소개해보았습니다. 다음 회차에서는 또 다른 예제 데이터를 사용하여 감마 보정을 적용하는 사례를 살펴보기로 하겠습니다.
* 감마 변수(gamma)의 값이 1보다 작을 경우 및 클 경우에 대한 설명 문구를 일부 수정한 후 다시 올립니다.
* 이 글이 도움이 되었다면 게시물에 대하여 공감 버튼(하트 모양) 클릭 및 블로그 구독도 해주시면 더 큰 힘이 됩니다. 감사합니다.
'IDL > Image Processing' 카테고리의 다른 글
| 감마 보정 (Gamma Correction) [2] (1) | 2026.01.15 |
|---|---|
| COLORTABLE 함수를 이용한 컬러테이블의 생성 [3] (0) | 2024.09.12 |
| COLORTABLE 함수를 이용한 컬러테이블의 생성 [2] (0) | 2024.09.03 |
| MORPH_OPEN 및 MORPH_CLOSE 함수 소개 (0) | 2024.08.08 |
| DILATE 함수 소개 (0) | 2024.08.01 |