IDL에서 플롯(Plot) 계열의 그림을 표출할 때 표시되는 선(Line)은 통상적으로는 단일 색상으로 나타내는 경우가 많습니다. 하지만 필요에 따라서는 선 자체를 여러가지 색상들로 구성되는 다중 색상의 선(Multi-Colored Line)의 형태로 구현하는 것도 가능합니다. 오늘은 그러한 처리 방법을 예제와 함께 살펴보기로 하겠습니다.
플롯의 선을 다중 색상으로 구현하는데 있어서는 PLOT 함수를 VERT_COLORS 및 RGB_TABLE 속성과 함께 사용하는 것이 기본적인 방법입니다. 이 방법을 간단한 예제와 함께 살펴봅시다. 먼저 플롯을 위한 예제 데이터를 생성하고 기본적인 표출까지 해보는 과정을 다음과 같이 정의해봅시다.
n = 200
x = FINDGEN(n)
y = SIN(x*!PI/100)*EXP(-0.02*x)+0.5
v = FINDGEN(n)/2
p = PLOT(x, y, THICK=5, XTICKLEN=0.02, YTICKLEN=0.02, $
XRANGE=[-10,210], YRANGE=[0.3,1], FONT_SIZE=11, $
MARGIN=0.1, /CURRENT)
이와 같이 200개의 값들로 구성되는 1차원 배열의 형태로 데이터 배열들(x, y, v)을 생성합니다. 이러한 데이터들에 대하여 PLOT 함수를 사용하여 기본적인 표출까지 진행해보면 그 모습은 다음과 같습니다.

그런데 위에서 x, y와 함께 정의한 v라는 배열은 그 값의 범위가 0~100이며 선을 구성하는 점들마다 별도의 데이터 값이 존재하는 상황을 가정한 것입니다. 그러면 선을 따라서 v의 값이 계속 변화하게 되는데, 이러한 변화를 색상에 대응시킨다면 플롯 라인이 마치 컬러바처럼 보이도록 v 데이터를 선의 색상으로 적용할 수 있게 됩니다. 이러한 방식의 구현을 위해서는 PLOT 함수의 내용에 다음과 같이 VERT_COLORS 및 RGB_TABLE 속성을 추가하면 됩니다.
p = PLOT(x, y, RGB_TABLE=34, VERT_COLORS=BYTSCL(v), $
THICK=5, XTICKLEN=0.02, YTICKLEN=0.02, $
XRANGE=[-10,210], YRANGE=[0.3,1], $
FONT_SIZE=11, MARGIN=0.1, /CURRENT)
이러한 변동사항을 반영하고 다시 실행하여 얻은 결과를 보면 그 모습은 다음과 같습니다.

이것은 배열 v의 값들을 바이트 스케일링하여 34번 컬러테이블의 색상들로 대응시킨 결과입니다. 그리고 이러한 그림의 특성을 감안하면 다음과 같이 컬러바도 추가하는 것이 좋을 것입니다.
cb = COLORBAR(POSITION=[0.2, 0.94, 0.8, 0.97], $
RANGE=[MIN(v), MAX(v)], /BORDER)
p.Translate, 0, -0.03, 0, /NORMAL
이러한 내용까지 반영하여 다시 실행하여 얻은 그림은 다음과 같습니다.
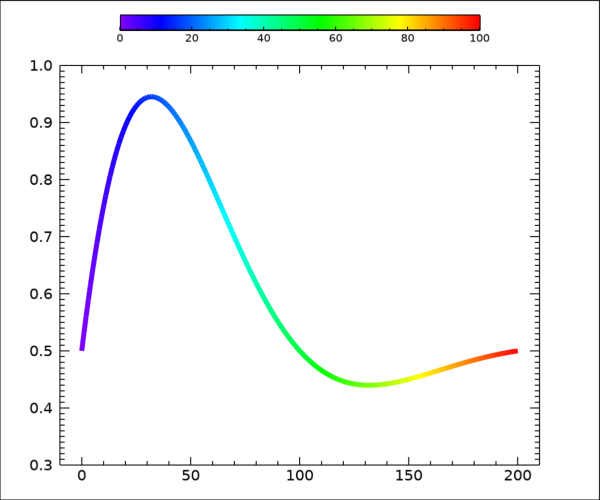
방금 소개한 예제를 보면 데이터 포인트들의 갯수가 200개로 그리 적은 편은 아닙니다. 그런데 데이터 포인트들의 갯수가 적은 경우에는 선을 다중 색상으로 구현하는데 있어서 약간의 문제(?)가 발생합니다. 그러한 예제로서 이번에는 달랑 5개의 데이터 포인트들만으로 구성된 예제 데이터를 가정해보겠습니다.
x = [0.8, 1, 2.1, 2.9, 4.3]
y = [0.2, 1.1, 2.4, 1.6, 1.2]
v = [10, 20, 30, 40, 50]
이러한 데이터를 대상으로 앞선 예제와 동일한 방식으로 표출까지 다음과 같이 진행해봅시다.
win = WINDOW(DIMENSIONS=[600, 500], /NO_TOOLBAR)
p = PLOT(x, y, RGB_TABLE=34, VERT_COLORS=BYTSCL(v), $
THICK=5, XTICKLEN=0.02, YTICKLEN=0.02, $
XRANGE=[0, 5], YRANGE=[0, 3], $
FONT_SIZE=11, MARGIN=0.1, /CURRENT)
cb = COLORBAR(POSITION=[0.2, 0.94, 0.8, 0.97], $
RANGE=[MIN(v), MAX(v)], /BORDER)
p.Translate, 0, -0.03, 0, /NORMAL
이와 같이 표출 작업을 진행해보면 그 결과는 다음 그림과 같습니다.
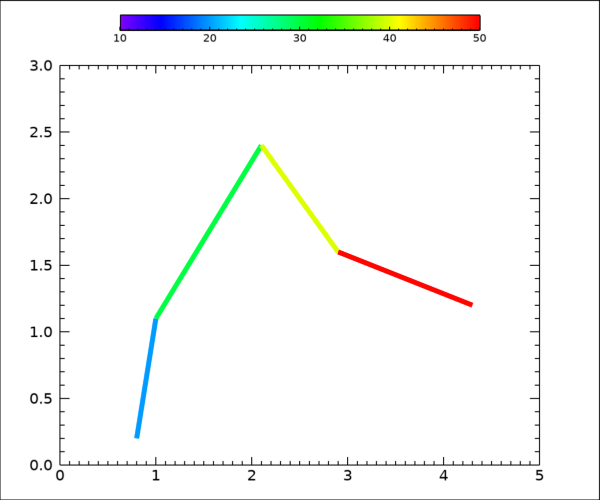
이 그림을 보면 플롯 라인의 색상들이 상당히 불연속적으로 반영된 것이 눈에 띕니다. 사실 이러한 결과 자체는 틀리지 않습니다. 원래 플롯의 선에 대하여 다중 색상이 반영되는 방식은 이와 같이 컬러테이블의 색상들 중 각 포인트별 데이터 값(여기서는 v)에 따라 적절한 간격으로 선택된 색상들이 사용되는데, 지금과 같이 데이터 포인트들의 갯수가 적을 경우에는 색상들이 상당히 띄엄띄엄 선택되기 때문에 위와 같이 선 자체의 색상들이 불연속적인 모습으로 보이는 것이 당연합니다. 즉 컬러테이블에는 256개의 색상들이 존재하는데 이에 대응되는 배열 v에는 5개의 값들만 존재하기 때문에 결국 256개의 색상들 중 5개만 적절한 간격으로 샘플링되어 사용되었기 때문이라고 보면 됩니다.
그런데 만약 이렇게 데이터 포인트 갯수가 적은 경우라 하더라도 그 선에 적용된 다중 색상이 마치 컬러바와 같이 부드럽게 변화하도록 처리하고 싶을 수도 있습니다. 물론 이러한 처리도 가능한데, 이를 위해서는 추가적인 내삽(Interpolation) 처리가 필요합니다. 즉 원래 5개에 불과한 데이터 포인트 갯수를 대폭 증가시킨 데이터를 따로 생성하여 사용하는 것입니다. 예를 들면 앞서 이미 생성했던 x, y, v를 이용하여 다음과 같은 처리를 추가적으로 수행합니다.
n = 300
xi = INTERPOL(x, n)
yi = INTERPOL(y, n)
vi = INTERPOL(v, n)
즉 여기서는 INTERPOL 함수를 사용하여 선형 내삽에 의하여 5개 짜리 배열을 300개 짜리 배열로 팽창(?)시키고 이 데이터를 이후의 표출 과정에 반영하는 방식으로 처리하였습니다. 그 다음에는 앞서 이미 제시했던 표출 과정에 x, y, v 대신 xi, yi, vi를 투입하면 됩니다. 다소 편법(?)스러운 느낌은 없지는 않지만 어쨌든 그 결과는 다음 그림과 같습니다.
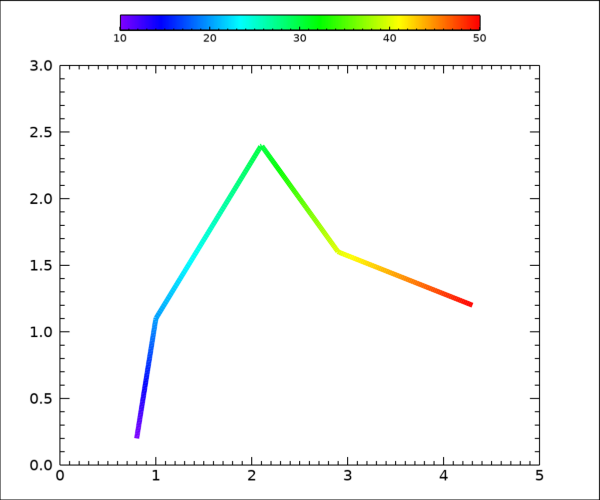
어쨌든 이와 같은 방식으로 처리하면 데이터 포인트들의 갯수가 적더라도 색상이 부드럽게 변화하는 다중 색상 플롯을 얻을 수 있습니다.
그리고 지금까지 제시된 처리 방법은 2차원 플롯 뿐 아니라 3차원 플롯에 대해서도 적용이 가능합니다. 즉 PLOT 함수 뿐 아니라 PLOT3D 함수에서도 처리 방식은 거의 유사합니다. 이와 같이 3차원 플롯 라인에 대하여 다중 색상을 적용한 예제를 보면 다음과 같습니다.
t = [-7.4:-0.4:0.01]
n = N_ELEMENTS(t)
x = 0.9*SIN(t)
y = 0.9*COS(1.6*t)
z = FINDGEN(n)/100
v = FINDGEN(n)/70
win = WINDOW(DIMENSIONS=[600, 600], /NO_TOOLBAR)
p = PLOT3D(x, y, z, RGB_TABLE=75, VERT_COLORS=BYTSCL(v), $
THICK=10, XRANGE=[-1, 1], YRANGE=[-1, 1], $
AXIS_STYLE=2, MARGIN=0.2, /CURRENT)
cb = COLORBAR(POSITION=[0.2, 0.94, 0.8, 0.97], $
RANGE=[MIN(v), MAX(v)], /BORDER, $
TITLE='Data Value', FONT_SIZE=11)
p.Translate, 0, 0, -0.05, /NORMAL
여기서 사용된 예제 데이터를 보면 위치 좌표 배열인 x, y, z 및 각 포인트별 데이터 값들로 구성된 배열 v로 구성됩니다. 각 배열은 701개의 값들로 구성된 1차원 배열이며, 배열 v의 값 범위는 0~10입니다. 그리고 PLOT3D 함수가 사용된 내용을 보면 다중 색상을 구현하는 방식 자체는 앞서 제시된 2차원 예제에서 PLOT 함수가 사용된 내용과 거의 동일하다는 것을 확인할 수 있습니다. 이 내용을 실행하면 표출 결과는 다음 그림과 같습니다.

* 이 글이 도움이 되었다면 게시물에 대하여 공감 버튼(하트 모양) 클릭 및 블로그 구독도 해주시면 더 큰 힘이 됩니다. 감사합니다.
'IDL > New Graphics' 카테고리의 다른 글
| 축(Axis)의 범위 뒤집기 (0) | 2025.10.01 |
|---|---|
| 막대 그래프(BarPlot)를 수평 방향으로 표출하기 (0) | 2025.09.29 |
| NG 체계의 컬러 명칭 목록 보기 (0) | 2025.09.10 |
| POLARPLOT 함수 소개 [2] (0) | 2025.04.29 |
| 색상을 채운 플롯(Filled Plot)의 표출 [2] (0) | 2025.03.13 |