얼마전에 GAUSSFIT 함수를 사용하여 Gaussian 근사를 하는 방법을 소개하는 게시물을 올린 바 있는데요. 오늘은 그 2차원 버전에 해당되는 GAUSS2DFIT 함수를 사용하여 2차원 Gaussian 근사를 하는 방법을 소개해보기로 하겠습니다. 즉 2차원 데이터가 나타내는 패턴을 2차원 Gaussian 함수에 맞춰서 근사하는데 있어서 GAUSS2DFIT 함수를 사용하는 방법이 될텐데요. IDL 도움말에서 GAUSS2DFIT 함수에 관한 내용을 보면 그 근거가 되는 수식에 관하여 다음과 같이 자세히 소개되어 있습니다.

즉 2차원 타원형 Gaussian 수식이라고 볼 수 있는데요. 2차원적인 패턴을 타원의 형태로 근사하고 그 타원의 장반경, 단반경, 중심점, 기울기 등에 해당되는 인자들을 근사에 의하여 산정하게 됩니다. 그러면 예제를 통하여 구체적으로 살펴보도록 하겠습니다. 먼저 예제용 데이터는 다음과 같이 HANNING 및 RANDOMN 함수를 활용하여 128x100의 구조를 갖는 2차원 배열로 생성합니다.
nx = 128
ny = 100
z = HANNING(nx, ny)*10+5+RANDOMN(-1, nx, ny)
HELP, z
PRINT, MIN(z), MAX(z)
이렇게 하면 전반적으로는 가운데 부분의 값이 높은 전형적인 HANNING 함수의 형태를 보이면서도 약간의 잡음(Noise)들도 가미된 모습의 2차원 데이터를 생성할 수 있습니다. 먼저 생성된 2차원 배열 z와 관련하여 출력된 값들을 보면 다음과 같습니다.
Z FLOAT = Array[128, 100]
1.43652 16.9128
이와 같이 z는 128x100의 2차원 구조를 가지며 값의 범위는 대략 1.4~16.9 정도인 것을 확인할 수 있습니다. 이번에는 배열 z의 모습을 이미지의 형태로 표출해봅시다. 그 과정은 다음과 같습니다.
win1 = WINDOW(DIMENSIONS=[nx, ny]*5, /NO_TOOLBAR)
im1 = IMAGE(z, MIN_VALUE=0, MAX_VALUE=20, $
AXIS_STYLE=2, MARGIN=0.1, FONT_SIZE=11, /CURRENT)
그리고 표출된 모습은 다음 그림과 같습니다.

이와 같이 예제 데이터 z는 마치 산봉우리가 솟아있는 것처럼 가운데 부분의 값이 높은 peak의 형태를 보입니다. 이제 이 예제 데이터 z에 대하여 GAUSS2DFIT 함수를 적용하여 근사 결과를 얻어봅시다. 그 과정은 다음과 같습니다.
zfit = GAUSS2DFIT(z, a, /TILT)
PRINT, 'Result : ', STRING(a, FORMAT='(7f8.3)')
계산의 결과는 GAUSS2DFIT 함수의 두번째 인수인 a라는 항목 그리고 그 좌변에 있는 zfit이라는 항목을 통하여 얻게 됩니다. 먼저 a는 2차원 Gaussian 수식을 구성하는 7개의 계수값들로 구성된 배열이 됩니다. 이 값들의 개요는 다음과 같습니다.
A[0] : constant term
A[1] : scale factor
A[2] : Gaussian width (X direction)
A[3] : Gaussian width (Y direction)
A[4] : center X location
A[5] : center Y location.
A[6] : rotation angle of the ellipse from the X axis in radians, counter-clockwise.
실제로 출력된 계수값들을 보면 다음과 같습니다.
Result : 4.615 10.761 26.929 21.115 63.858 49.947 -0.009
그리고 zfit은 위의 계수값들이 투입된 2차원 Gaussian 수식에 의하여 산출된 근사 결과에 해당되는 2차원 배열입니다. 그러므로 zfit의 배열 구조는 원본 데이터인 z와 동일하지만 그 값들은 계산된 근사값들에 해당됩니다. 이제 다음과 같이 별도의 그래픽창을 띄워서 이 결과를 이미지의 형태로 표출해봅시다.
win2 = WINDOW(DIMENSIONS=[nx, ny]*5, /NO_TOOLBAR)
im2 = IMAGE(zfit, MIN_VALUE=0, MAX_VALUE=20, $
AXIS_STYLE=2, MARGIN=0.1, FONT_SIZE=11, /CURRENT)
그리고 표출된 모습은 다음 그림과 같습니다.
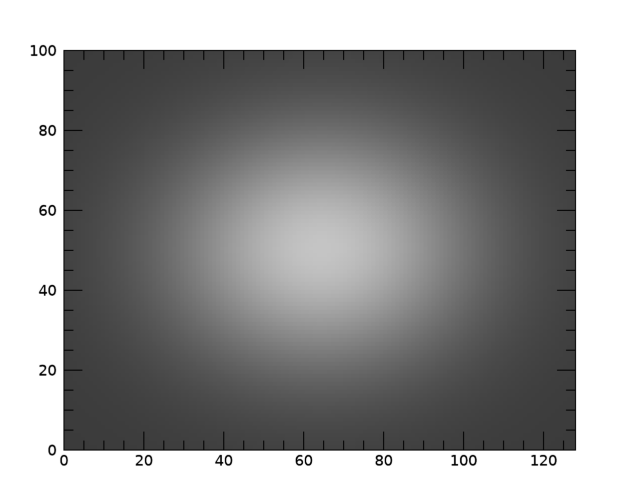
앞서 원본 데이터인 z를 표출한 모습과 지금 zfit를 표출한 모습을 서로 비교해보면, 나름대로 서로 유사한 모습을 보입니다. 따라서 그럴싸한 근사 결과를 얻었음을 확인할 수 있습니다. 보다 직접적인 비교를 위하여 근사결과 데이터인 zfit에 대한 등위선(Contour)을 원본 데이터인 z의 이미지 상에 다음과 같이 중첩해봅시다.
im1.Select
c1 = CONTOUR(zfit, C_VALUE=[6, 9, 12], C_LABEL_SHOW=1, $
COLOR='cyan', C_THICK=2, FONT_SIZE=11, /OVERPLOT)
그 모습은 다음 그림과 같습니다.

여기서 잠깐만. 우리가 앞서 a라는 배열로 얻었던 결과, 즉 2차원 Gaussian 수식을 구성하는 7개의 계수값들로 구성된 배열의 값들을 이 시점에서 다시 좀 살펴볼 필요가 있습니다. 우선 앞서 출력했던 결과값들은 다음과 같습니다.
Result : 4.615 10.761 26.929 21.115 63.858 49.947 -0.009
이 값들을 좀 살펴보자면, 먼저 근사된 타원의 중심 좌표는 대략 (63.86, 49.95)이며, X축 방향을 기준으로 한 타원의 회전각도는 거의 0에 가깝습니다. 그리고 X 방향 및 Y 방향의 Gaussian width는 각각 약 29.9 및 21.1 정도로 산출되었습니다. 이러한 숫자들에 대해서는, 방금 표출한 그림을 보면서 따져본다면 그 값들이 충분히 근거가 있음을 눈으로도 확인할 수 있을 것입니다.
그리고 원본 데이터와 근사 결과의 유사성을 보기 위하여 다음과 같이 서피스(Surface)의 형태로 표출하여 비교해보는 것도 괜찮습니다.
win_sf = WINDOW(DIMENSIONS=[800, 300], /NO_TOOLBAR)
sf1 = SURFACE(z, ZRANGE=[0, 20], /CURRENT, LAYOUT=[2, 1, 1])
sf2 = SURFACE(zfit, ZRANGE=[0, 20], /CURRENT, LAYOUT=[2, 1, 2])
sf1.Rotate, /RESET
sf1.Rotate, 15, /XAXIS
sf1.Rotate, 15, /YAXIS
sf1.Rotate, -90, /XAXIS
sf2.Rotate, /RESET
sf2.Rotate, 15, /XAXIS
sf2.Rotate, 15, /YAXIS
sf2.Rotate, -90, /XAXIS
여기서는 그래픽창을 띄우고 왼쪽에는 z 오른쪽에는 zfit에 대하여 각각 SURFACE 함수를 적용하여 표출하였습니다. 다만 서피스의 시선 방향을 디폴트와는 약간 다르게 조정하는 것이 필요할 것 같아서, 각각에 대하여 Rotate 메서드를 사용하여 시선 방향을 조정하였습니다. 그 모습은 다음 그림과 같습니다.

이러한 표출을 통해서도 원본 데이터와 근사 결과 사이의 유사성을 눈으로 확인할 수 있을 것입니다. 이 예제에서 사용된 예제 데이터는 위 그림에서 볼 수 있듯이 가운데 부분의 값이 높게 솟아있는(마치 산봉우리와 같은) peak의 형태인데요. 만약 가운데 부분의 값이 낮은 (마치 골짜기와 같은) valley의 형태일 경우에는 어떻게 하면 될까요? 그 경우에는 GAUSS2DFIT 함수를 사용할 때 반드시 /NEGATIVE 키워드를 함께 사용해야 합니다. 왜냐하면 GAUSS2DFIT 함수는 기본적으로는 데이터가 peak의 형태인 경우를 가정하고 계산을 수행하기 때문입니다. 이러한 예도 한번 보기 위하여, 원본 예제 데이터 배열인 z를 다음과 같이 valley의 형태가 되도록 다시 정의해봅시다.
z = -HANNING(nx, ny)*10+15+RANDOMN(-2, nx, ny)
나머지 처리 과정은 앞서 소개된 내용과 거의 동일합니다. 다만 한가지 중요한 차이점은 앞서 언급했듯이 GAUSS2DFIT 함수를 사용하면서 반드시 /NEGATIVE 키워드를 추가해야 한다는 것입니다.
zfit = GAUSS2DFIT(z, a, /TILT, /NEGATIVE)
따라서 위의 두가지 변경사항만 반영하고 나머지 내용은 그대로 살려서 실행하면 됩니다. 그러면 실행 결과를 봅시다. 먼저 산출된 7개의 계수값들은 다음과 같습니다.
Result : 15.386 -10.829 26.894 20.863 64.049 50.056 -0.014
여기서는 데이터의 패턴이 valley 형태이기 때문에 두번째 계수인 a[1]의 값이 (-)가 된다는 점을 주목하면 됩니다. 그리고 결과 그림들은 다음과 같습니다. 먼저 원본 데이터의 모습입니다.

그리고 근사 결과의 모습입니다.
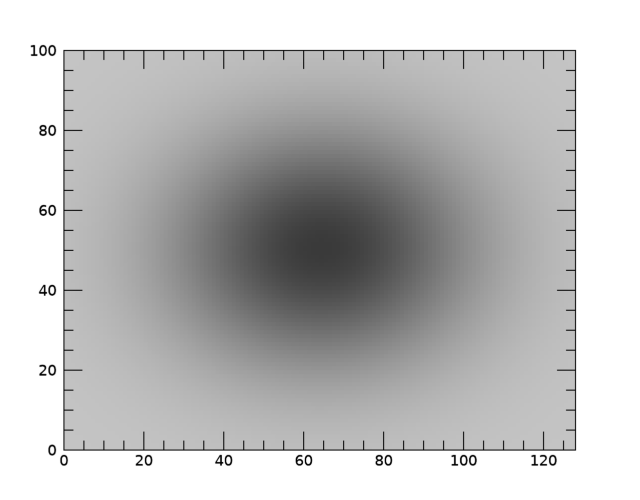
원본 데이터 이미지에 근사 결과 등위선(Contour)을 중첩한 모습은 다음과 같습니다.

그리고 원본 데이터와 근사 결과를 서피스(Surface)의 형태로 표출하여 서로 비교한 모습은 다음과 같습니다.

대략 이 정도면 GAUSS2DFIT 함수를 이용하여 2차원 Gaussian 근사 결과를 얻는 방법에 대해서는 충분히 소개된 것 같습니다. IDL 도움말에서 GAUSS2DFIT 함수에 관한 내용을 보면 또 다른 예제 데이터에 대하여 적용된 경우에 대해서도 소개되어 있으므로 이 내용도 함께 참조하시면 좋을 것 같습니다.
'IDL > Math' 카테고리의 다른 글
| INTERPOL 함수를 이용한 1차원 내삽(1-d Interpolation) (0) | 2021.07.26 |
|---|---|
| MEDIAN 함수에 의한 중간값 산출에 관한 유의사항 (0) | 2021.06.18 |
| GAUSSFIT 함수를 이용한 Gaussian 함수 근사 (0) | 2020.12.28 |
| 구면상의 지점 분포 데이터에 대한 격자화 및 유의사항 (0) | 2020.12.18 |
| NaN, Infinity와 FINITE 함수 (0) | 2020.08.10 |