오늘은 IDL에서 Quick Hull 알고리즘을 사용할 수 있게 해주는 QHULL 프로시저를 소개해보고자 합니다. 이 알고리즘은 2차원 이상의 공간 내에서 다수의 점들이 분포하는 상태에서 Quick Hull 알고리즘에 의하여 이 점들을 모두 포함하는 최대 크기의 볼록 다각형(Largest Convex Polygon)을 찾아내는 기법입니다. 그러면 2차원 공간 내에 존재하는 임의의 점들을 가정하여 그 과정을 살펴보기로 하겠습니다. 먼저 다음과 같이 10개의 점들로 구성된 가상 데이터를 생성하고 이 점들을 2차원 공간상에 표시해봅시다.
x1 = RANDOMU(-1, 10)*10
y1 = RANDOMU(-2, 10)*10+50
win = WINDOW(DIMENSIONS=[600, 600], /NO_TOOLBAR)
p = PLOT(x1, y1, SYMBOL='circle', /SYM_FILLED, SYM_SIZE=0.7, $
LINESTYLE=6, TITLE='QHULL Test', COLOR='crimson', $
MARGIN=0.1, FONT_SIZE=11, /CURRENT)
FOR j = 0, N_ELEMENTS(x1)-1 DO $
tx = TEXT(x1[j]+0.05, y1[j]+0.05, STRTRIM(STRING(j), 2), /DATA)
여기서는 PLOT 함수로 구현된 2차원 공간상에 10개의 점들을 표시한 다음, TEXT 함수를 사용하여 각 점의 일련번호도 함께 표시하였습니다. 이러한 과정에 의하여 표출된 그림은 다음과 같습니다.

이제 여기서 QHULL 프로시저를 다음과 같이 사용하면 됩니다.
QHULL, x1, y1, t
HELP, t
PRINT, 'Output list of vertices (t variable) from QHULL: '
PRINT, t
먼저 QHULL 명령에 대해서는 점들의 좌표인 x1, y1 그리고 결과를 받아올 t를 인수로 투입하였습니다. HELP 및 PRINT에 의하여 출력된 내용을 보면 다음과 같습니다.
T LONG = Array[2, 5]
Output list of vertices (t variable) from QHULL:
8 1
3 8
2 3
7 2
1 7
일단 t는 2x5의 구조를 갖는 2차원 배열입니다. 이것은 10개의 점들을 모두 포함하는 최대 크기의 볼록 다각형을 구성하는 선들이 어떤 식으로 이어지는가 즉 다각형을 구성할 점들의 연결성에 대한 정보라고 보면 됩니다. 즉 8번 점과 1번 점이 이어지고, 3번 점과 8번 점이 이어지는 등과 같은 연결성을 나타내기 때문에 이와 같이 점들을 이어주면 최대 크기의 다각형이 될 것임을 알 수 있습니다. 다만 이와 같이 t에 담겨진 정보만으로는 이어질 점들의 순서가 완벽하지는 않습니다. 따라서 순서에 맞게 재정돈하는 과정이 필요합니다. 그 과정은 다음과 같이 처리하면 됩니다.
verts = INTARR(N_ELEMENTS(t[0, *])+1)
verts[0] = t[0, 0]
verts[1] = t[1, 0]
FOR i = 1, N_ELEMENTS(t[0, *])-1 DO BEGIN
id = WHERE(t[0, *] EQ verts[i])
verts[i+1] = t[1, id]
ENDFOR
HELP, verts
PRINT, 'Polygon vertices order: ', verts
과정 자체가 다소 복잡해보이는 감은 있지만 출력된 결과를 보면 다음과 같습니다.
VERTS INT = Array[6]
Polygon vertices order: 8 1 7 2 3 8
이와 같이 최대 크기 볼록 다각형을 구성하는 점들이 이어지는 순서에 대한 정보를 정확히 담은 결과인 verts를 얻을 수 있습니다. 이제 다음과 같이 원래 데이터인 x1, y1에 대하여 이 verts 배열로 인덱싱을 합니다.
x2 = x1[verts]
y2 = y1[verts]
그러면 이와 같이 순서에 맞는 점들로 구성된 x2, y2를 얻게 됩니다. 이들을 다음과 같이 PLOT 함수에 투입하면 선들로 이어진 다각형을 중첩하여 표시할 수 있습니다.
pl = PLOT(x2, y2, LINESTYLE=0, COLOR='blue', /OVERPLOT)
이 과정까지 추가로 실행되어 표출된 그림은 다음과 같습니다.
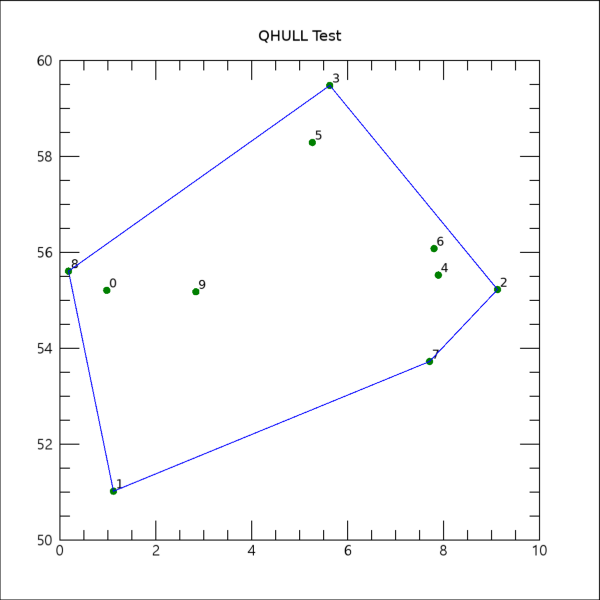
이와 같이 주어진 모든 점들에 대하여 이들을 포함하는 최대 크기의 볼록 다각형을 얻을 수 있습니다. 따라서 지금까지의 과정은 QHULL 프로시저의 Quick Hull 알고리즘에 의하여 산출된 결과를 다듬어서 가시화하는 과정이라고 보면 됩니다. 그리고 이 결과를 이용하여 다각형의 중심점의 위치를 얻는 것도 가능합니다. 이 과정은 IDLanROI 객체를 이용하면서 ComputeGeometry 메서드 및 CENTROID 키워드를 활용하는 방식으로 처리하면 되는데, 이러한 방법에 관해서는 예전에 관련 게시물에서 잠깐 언급한 적이 있습니다. 어쨌든 그 과정은 다음과 같습니다.
roi = IDLanROI()
roi.SetProperty, DATA=TRANSPOSE([[x2],[y2]])
a = roi.ComputeGeometry(CENTROID=cen)
HELP, cen
PRINT, cen
이와 같이 얻은 결과인 cen에 대하여 출력된 내용을 보면 다음과 같습니다.
CEN DOUBLE = Array[3]
4.3165903 55.145074 0.0000000
이와 같이 중심점의 좌표는 (X, Y, Z)의 형태로 얻어지는데 어차피 이번 예제는 2차원 데이터이므로 (X, Y) 좌표만 확인하면 됩니다. 이 값들을 이용하여 중심점의 위치를 추가하여 표시해봅시다. 그 과정은 다음과 같습니다.
pc = SYMBOL(cen[0], cen[1], 'circle', /SYM_FILLED, $
SYM_COLOR='crimson', /DATA)
이러한 과정까지 추가로 실행되면 결과는 다음 그림과 같습니다.

따라서 QHULL 프로시저를 활용하여 다수의 점들에 대하여 이들을 모두 포함하는 최대 크기의 다각형에 대한 정보를 산출하고 관련 표출을 하는 방법은 대략 위와 같습니다. 그리고 초반에 이미 언급했듯이 QHULL 프로시저는 2차원 이상인 다차원 공간 데이터에 대해서도 적용이 가능합니다. 즉 3차원 공간상에 분포하는 다수의 점들에 대해서도 결과를 얻을 수 있습니다. 3차원 데이터에 대한 예제는 나중에 기회가 되면 다뤄보기로 하겠습니다.
그리고 오늘 소개된 내용은 얼마전 NV5 Geospatial 웹페이지에 올라왔던 게시물의 내용을 참조하였음을 밝혀둡니다. 해당 링크는 아래와 같습니다.
이 글이 도움이 되었다면 게시물에 대하여 공감 버튼(하트 모양) 클릭 및 블로그 구독도 해주시면 더 큰 힘이 됩니다. 감사합니다.
'IDL > Programming' 카테고리의 다른 글
| CASE 구문과 SWITCH 구문 (0) | 2025.05.20 |
|---|---|
| QHULL 함수를 이용하여 최대 볼록 다각형 찾기 (3차원) (0) | 2025.05.14 |
| Permil 기호의 표시 featuring 유니코드 문자 사용법 (0) | 2025.04.22 |
| Yale Bright Star Catalog 데이터 읽기 (개선된 방법) (0) | 2025.04.15 |
| Yale Bright Star Catalog 데이터를 읽고 처리하기 [4] (1) | 2025.04.08 |