우리가 데이터 처리를 하다보면 불규칙한 간격으로 분포하고 있는 1차원 데이터를 규칙적인 간격의 1차원 데이터로 변환하는 것이 필요할 경우가 종종 있습니다. 물론 IDL에서도 이러한 처리가 가능한데 바로 INTERPOL 함수가 그러한 역할을 합니다. 참고로 INTERPOL 함수에 관해서는 제가 예전에 관련 게시물을 통하여 이미 소개를 한 바 있으며, 오늘 소개될 내용은 그 연장선에 있다고 보시면 됩니다. 그러면 예제 데이터와 함께 이러한 처리 방법을 살펴보겠습니다. 먼저 예제로 사용할 1차원 데이터는 다음과 같이 x 및 y라는 배열로 정의해봅니다.
x = [1.2, 3.8, 4.9, 7.2, 8.5, 9.6, 12.4]
y = [39.16, 82.46, 86.93, 44.41, 15.68, 5.89, 22.94]
여기서 배열 x의 값들을 보면 그 간격이 일정하지 않음을 알 수 있습니다. 일단 이러한 데이터를 간단하게 표출해봅시다. 그 과정 및 표출 결과는 다음과 같습니다.
win = WINDOW(DIMENSIONS=[600, 500], /NO_TOOLBAR)
p = PLOT(x, y, LINESTYLE=6, SYMBOL='circle', $
/SYM_FILLED, SYM_SIZE=1.5, COLOR='blue', $
FONT_SIZE=11, MARGIN=0.1, /CURRENT)

이와 같이 불규칙한 간격으로 분포하는 1차원 데이터에 대하여 INTERPOL 함수를 사용하여 일정한 간격의 1차원 데이터로 변환해봅시다. 먼저 일정한 간격의 X축 값들로 구성된 배열을 정의해두는 것이 필요합니다. 이러한 배열도 INTERPOL 함수에 투입되어야 하기 때문입니다.
xf = [1:13:0.5]
이렇게 정의된 xf는 1부터 13까지 0.5의 일정한 간격을 갖는 실수형 값들로 구성됩니다. 이제 INTERPOL 함수를 다음과 같이 사용하면 됩니다.
yf = INTERPOL(y, x, xf)
앞서 정의된 y, x, xf 배열들이 차례로 인수로 투입되었음을 유의해야 합니다. 이렇게 하면 앞서 정의된 배열 xf의 값들에 대응되는 Y축의 값들이 배열 yf로 얻어집니다. 그러면 xf, yf 데이터를 같은 XY축 공간상에 플롯의 형태로 중첩하는 것이 좋을 것입니다. 그 과정은 다음과 같이 처리해봅시다.
po = PLOT(xf, yf, LINESTYLE=6, SYMBOL='circle', $
/SYM_FILLED, SYM_SIZE=1.2, COLOR='tomato', /OVERPLOT)
표출 결과는 다음과 같습니다.
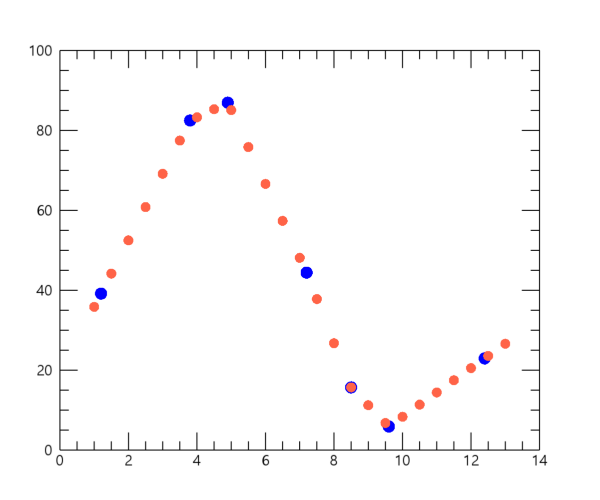
그런데 이 결과를 잘 보면 내삽의 결과가 너무 좀 투박하다는 느낌이 들 것입니다. 그럴 수 밖에 없는 것이 INTERPOL 함수의 기본 설정이 선형 내삽(Linear Interpolation)이기 때문입니다. 따라서 다른 방식의 내삽을 적용해보는 것이 어떨까 싶습니다. 앞서 INTERPOL 함수가 사용되었던 내용을 다음과 같이 변경해봅시다.
yf = INTERPOL(y, x, xf, /SPLINE)
여기서는 INTERPOL 함수에 의한 내삽이 Spline Interpolation 기법에 의하여 수행되도록 하기 위하여 /SPLINE 키워드를 추가한 것입니다. 이러한 기법을 적용하면 좀 더 부드럽게 이어지는 결과를 얻을 수 있습니다. 이렇게 다시 얻은 xf, yf를 적용하여 바로 위의 PLOT 함수가 사용된 내용을 다시 실행해보면 그 모습은 다음과 같습니다.
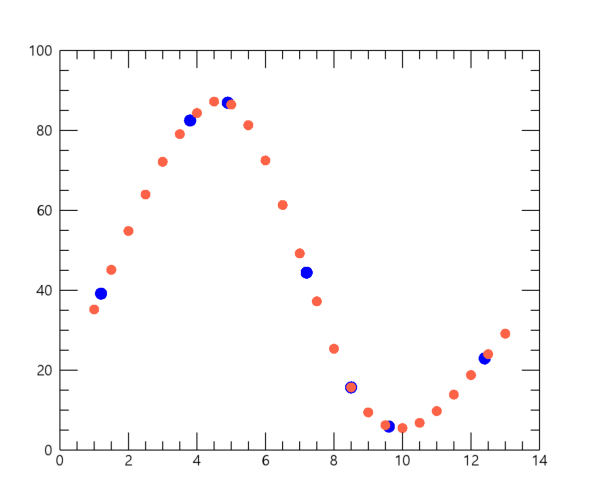
이 결과를 보면 앞서 INTERPOL 함수의 디폴트 설정인 선형 내삽에 의하여 얻은 결과에 비해서는 원래의 데이터 포인트들을 좀 더 부드럽게 이어주는 내삽 결과를 얻은 것 같습니다. 만약 위의 내용에서 새로 중첩되는 플롯을 심볼 대신 선의 형태로 바꿔보고자 한다면 위의 PLOT 함수가 사용된 내용만 대략 다음과 같이 변경해주면 됩니다.
po = PLOT(xf, yf, THICK=2, COLOR='tomato', /OVERPLOT)
표출 결과는 다음과 같습니다.

지금까지 불규칙한 간격으로 분포하는 1차원 데이터를 규칙적인 간격의 1차원 데이터로 변환하는데 있어서는 INTERPOL 함수를 사용하여 1차원 내삽을 적절한 기법으로 수행하여 결과를 얻으면 된다는 것을 관련 예제와 함께 살펴보았습니다. 물론 위의 예제와 같은 내삽의 결과가 100% 정확하다고 단정할 수는 없을 것입니다. 어떤 방식으로 내삽을 수행하여 결과를 얻는 것이 타당할 것인지는 데이터의 특성에 따라 연구자가 판단해야 할 것입니다.
'IDL > Math' 카테고리의 다른 글
| 각도의 변환 (십진수와 DMS 단위) : EOS_EH_CONVANG 함수 (1) | 2025.02.11 |
|---|---|
| TS_FCAST 함수 소개 (0) | 2024.08.21 |
| 플랑크(Planck) 복사량 법칙의 가시화 (1) | 2024.06.20 |
| VALUE_LOCATE 함수 소개 (0) | 2024.06.07 |
| 증가 및 감소 연산자 (Increment and Decrement Operator) (1) | 2023.11.20 |