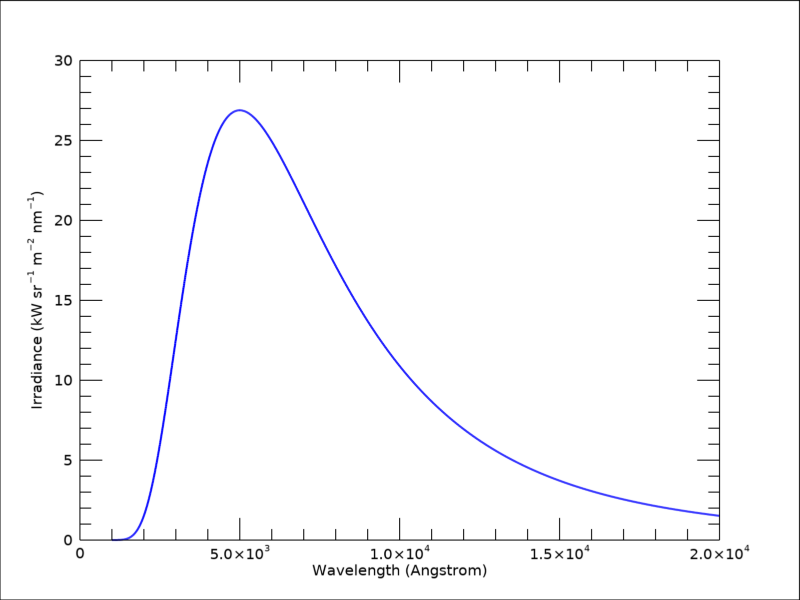
플랑크의 복사량 법칙(Planck's Radiation Law)은 잘 알려져있듯이 특정한 온도의 흑체(Black Body)로부터 방출되는 복사량을 모든 파장(또는 주파수)에 걸쳐서 계산하는 수식으로 표현됩니다. 그래서 이러한 수식을 플랑크 곡선의 형태로 표출한 그림은 각종 물리학 교과서나 웹페이지들에서 많이 볼 수 있습니다. 오늘은 플랑크 법칙을 기반으로 플랑크 곡선을 표출하는 작업을 IDL에서 직접 구현해보고자 합니다. 이 작업은 이론적인 수식을 프로그램에 반영하고 이를 기반으로 표출용 데이터를 생성하여 그림의 형태로 표출하는 일련의 과정이라고 볼 수 있습니다. 일단 결과의 티저부터 먼저 보면 대략 다음과 같은 그림을 표출해보고자 하는 것입니다.
일단 이 작업을 시작하기 위해서는 플랑크 법칙을 나타내는 수식을 살펴봐야 합니다. 사실 플랑크 법칙의 수식은 파장 또는 주파수를 기준으로 할 것이냐 및 구체적으로 어떤 물리량을 계산할 것이냐에 따라서 여러가지 종류가 있는데, 여기서는 파장(Wavelength)에 대하여 복사량(Irradiance)을 계산하는 수식을 사용하기로 합니다. 그 수식의 모습은 다음과 같습니다.
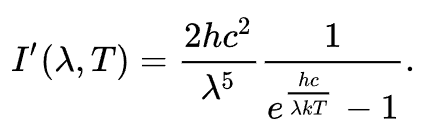
참고로 이 수식은 위키백과에서 퍼온 것입니다. 일단 여기서는 플랑크 상수(h), 빛의 속도(c) 그리고 볼츠만 상수(k)와 같은 물리상수들이 등장합니다. 이러한 상수들의 값은 IDL에도 이미 내장되어 있으므로 그대로 가져와서 활용하면 됩니다. 이 과정은 다음과 같이 처리해봅시다.
c = !const.c
h = !const.h
k = !const.k
이와 같이 각 상수의 값을 담은 변수 c, h, k를 정의합니다. 여기서는 IDL에서 각종 과학상수들을 내장한 !const로부터 각각의 상수를 끌어온 것입니다. 참고로 !const에 관한 더 자세한 내용은 관련 게시물을 참조하시기 바랍니다. 그리고 플랑크 법칙에서 온도는 절대온도 단위로 특정한 온도 값을 지정해야 하는데, 여기서는 태양의 표면 온도인 5800K를 사용하기로 합니다.
t = 5800.
그 다음에는 파장의 값들을 정의해야 합니다. 즉 수식을 반영하여 그림을 그리기 위해서는 적절한 파장 범위에 속하는 파장 값들로 구성된 배열을 생성하는 것이 필요합니다. 여기서는 100~2000(nm) 범위의 값들로 구성된 배열로 다음과 같이 정의하고자 합니다.
w = [100:2000:1.0]*1e-9
여기서는 파장의 값들을 m 단위로 환산하였음을 유의해야 합니다. 즉 앞서 언급한 과학상수들도 그렇고 지금 정의한 파장의 값들 모두 MKS 단위로 통일되도록 하는 것입니다. 이제 다음은 복사량의 계산 수식을 정의하고 여기에 파장 값 배열을 투입하여 계산되는 복사량 값들로 구성된 결과 배열을 얻어야 합니다. 이를 위해서는 위의 수식을 코딩으로 표현해야 할 것입니다. 그 과정은 다음과 같습니다.
rad = 2*h*c^2/w^5/(EXP(h*c/(w*k*t))-1)
여기서는 앞서 정의했던 요소들이 모두 투입된 수식에 의하여 복사량 값들로 구성된 배열 rad를 얻었습니다. 다만 여기서 끝나는 것이 아니고 복사량 값의 단위에서 W 대신 kW가 되도록 하고 파장으로 1 nm 당의 값이 되도록 환산하는 것이 필요하기 때문에 다음과 같은 환산 과정을 한번 더 거쳐야 합니다.
rad = rad*1e-9*1e-3
그리고 그림의 표출에 있어서 X축의 파장 값들이 Angstrom 단위로 보이는 것이 더 좋을 것 같으므로 파장값 배열도 다음과같은 환산 과정을 거치는 것이 좋을 것 같습니다.
wa = w*1e10
이제 그림의 표출 과정으로 넘어가면 됩니다. 기본적으로는 앞서 얻은 wa, rad 배열을 PLOT 함수에 투입하면 되는데, 구체적인 과정은 다음과 같이 처리해봅시다.
win = WINDOW(DIMENSIONS=[800, 600], /NO_TOOLBAR)
p = PLOT(wa, rad, COLOR='blue', THICK=2, $
XTITLE='Wavelength (Angstrom)', $
YTITLE='Irradiance ($kW sr^{-1} m^{-2} nm^{-1}$)', $
MARGIN=0.1, FONT_SIZE=11, /CURRENT)
tx = TEXT(0.5, 0.94, "Planck's Radiation Law (Temperature : "+$
STRING(t, FORMAT='(F0.1)')+' K)', $
ALIGNMENT=0.5, FONT_SIZE=14, /NORMAL)
이 과정을 실행하면 바로 다음과 같은 그림을 얻게 됩니다. 앞서 서두에서 제시했던 그림과 기본적으로는 동일하지만 타이틀 문자를 추가하였습니다.

그리고 아마 많이들 알고 계시겠지만, 가시광(Visible Light)의 파장 범위는 대략 3800~7400(Angstrom) 정도인 것으로 흔히 얘기합니다. 그래서 위의 그림에 이러한 가시광 영역의 스펙트럼을 이미지의 형태로 중첩해보는 것도 흥미로울 것 같습니다. 가시광 영역의 스펙트럼 이미지를 표시하기 위해서는 IDL의 컬러테이블들 중 Rainbow라는 명칭의 컬러테이블을 사용하면 무난합니다. 이 컬러테이블의 번호는 13번이며 그 색상 구성은 다음과 같습니다.

그래서 이러한 이미지를 앞서 플랑크 곡선 플롯 상에서 적절한 파장 범위에 위치하도록 중첩해보고자 합니다. 그 과정은 다음과 같이 처리해봅시다.
imc = BINDGEN(256)#REPLICATE(1, 50)
cb = IMAGE(imc, RGB_TABLE=13, $
IMAGE_LOCATION=[3800, 0], IMAGE_DIMENSION=[3600, p.YRANGE[1]], $
ASPECT_RATIO=0, /OVERPLOT)
여기서는 먼저 중첩할 이미지 배열인 imc를 정의하고 이를 IMAGE 함수에 투입하여 그 이미지가 플롯 상에 중첩되도록 한 것입니다. 플롯 상에서 이미지가 중첩될 위치를 명확히 지정하기 위하여 IMAGE_LOCATION 및 IMAGE_DIMENSION 속성을 사용하였음을 주목해야 합니다. 이 과정까지 실행되어 표출된 최종 결과 그림은 다음과 같습니다.

이와 같이 플랑크 곡선 플롯 상에 가시광 스펙트럼 이미지를 적절한 파장 범위에 중첩해본 그림을 얻어보았습니다. 물론 가시광 영역의 정확한 파장 범위라든지 각 색상별 파장 범위 등에 관한 좀 더 명확한 정보를 갖고 있을 경우에는 이러한 근거에 의하여 색상 구성이 반영된 이미지를 따로 만들어서 적용할 수도 있을 것입니다.
'IDL > Math' 카테고리의 다른 글
| 불규칙 간격의 1차원 데이터의 내삽 (0) | 2024.08.26 |
|---|---|
| TS_FCAST 함수 소개 (0) | 2024.08.21 |
| VALUE_LOCATE 함수 소개 (0) | 2024.06.07 |
| 증가 및 감소 연산자 (Increment and Decrement Operator) (1) | 2023.11.20 |
| K-평균 군집화 분석 (K-means Clustering) (0) | 2023.10.25 |