오늘은 IDL의 GAUSSFIT 함수를 이용하여 Gaussian 함수 근사를 수행하는 방법에 관하여 소개해보기로 하겠습니다. Gaussian 함수는 그 형태가 마치 종의 모양(Bell Shape)을 띄며, 기초통계에서 등장하는 정규분포함수 역시 이러한 형태를 띄는 것으로 잘 알려져 있습니다. 원래 이 함수의 일반적인 수식은 다음과 같습니다.
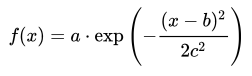
이 수식에서는 그 형태를 결정짓는 인자들이 a, b, c 세 개입니다. 그런데 IDL의 GAUSSFIT 함수에서는 이러한 3-term Gaussian 함수에 대한 근사 뿐만 아니라, 인자들이 더 많은 케이스들(4, 5, 6-term)에 대한 근사도 가능합니다. 즉 다음과 같이 기본적으로는 Gaussian의 형태를 가지면서 베이스라인의 형태가 다양한 일반적인 케이스들까지도 커버할 수 있습니다.
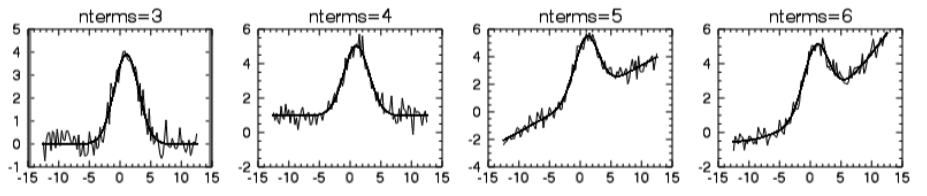
이와 같은 인수값에 따른 구분은 실제로 GAUSSFIT 함수 내에서 NTERMS라는 키워드를 통하여 설정하게 됩니다. 즉 이 키워드의 값은 3, 4, 5, 6 중 하나가 됩니다. 이 키워드의 디폴트값은 6입니다. 즉 별다른 지정을 하지 않으면 6-term Gaussian 함수를 가정하여 처리됩니다. 따라서 근사하고자 하는 Gaussian 함수의 형태에 따라서 이 키워드의 값을 직접 명시적으로 설정하는 것이 필요할 수도 있습니다. 각 케이스별 바탕 수식의 모습은 다음과 같습니다.

그러면 GAUSSFIT 함수를 사용하여 Gaussian 함수 근사를 수행하는 과정을 예제를 통하여 살펴봅시다. 먼저 예제 데이터의 경우는 원활한 설명을 위해서는 전반적으로 Gaussian 함수의 형태를 따르면서도 어느 정도 랜덤한 값들이 되도록 인위적으로 생성하는 것이 필요합니다. 따라서 다음과 같은 방식으로 생성하였습니다.
n = 101
x = (FINDGEN(n)-(n/2))/4
a = [4.0, 1.0, 2.0, 1.0, 0.25, 0.01]
print, 'Expect : ', a
z = (x - a[1])/a[2] ; Gaussian variable
seed = -5 ; Pick a starting seed value
y = 0.4*RANDOMN(seed, n)+a[0]*EXP(-z^2/2)
여기서는 먼저 X 데이터는 대략 -15~+15의 범위를 갖고 Y 데이터는 3-term Gaussian 함수의 형태를 대략 따르도록 하여, 101개의 값들로 구성된 x, y 배열을 생성하였습니다. 그리고 배열 a는 가상 데이터가 Gaussian 함수의 형태가 되도록 하기 위하여 가정하여 사용한 계수값들입니다. 나중에 GAUSSFIT 함수에 의하여 산출될 결과값들은 결국 이 a의 값들과 유사할 것입니다. 어느 정도까지 유사한 결과가 나올 것인지는 나중에 확인해보기로 합시다. 일단 이렇게 생성된 예제 데이터를 그림으로 표출해보면 다음과 같습니다.
win = WINDOW(DIMENSIONS=[600, 500], /NO_TOOLBAR)
p1 = PLOT(x, y, SYMBOL='circle', /SYM_FILLED, COLOR='green', $
TITLE='nterms : 3', MARGIN=0.1, /CURRENT)

그러면 이제 이러한 데이터에 대하여 GAUSSFIT 함수를 적용하여 근사 결과를 얻어봅시다. 그 방법은 다음과 같습니다.
yfit = GAUSSFIT(x, y, coeff, NTERMS=3)
PRINT, 'Result : ', coeff
이 과정을 거치면 그 결과는 coeff, yfit 두 배열로 산출됩니다. 먼저 coeff는 근사된 Gaussian 함수의 계수값들입니다. 위의 경우는 3-term이기 때문에 coeff는 세 개의 계수값들로 구성된 배열이 됩니다. 실제로 출력된 내용을 보면 다음과 같습니다.
Expect : 4.00000 1.00000 2.00000 1.00000 0.250000 0.0100000
Result : 3.86547 0.987056 2.06947
어차피 지금은 3-term인 경우이므로 처음 세 개의 값들만 서로 비교해보면 되는데, 어느 정도 유사한 계수값들이 산출되었음을 확인할 수 있습니다. 그리고 yfit은 이와 같이 근사된 함수에 의하여 계산된 101개의 Y값들로 구성된 배열입니다. 따라서 다음과 같이 그 형태를 중첩하여 표출해볼 수 있습니다.
p2 = PLOT(x, yfit, COLOR='red', THICK=3, /OVERPLOT)
그 모습은 다음 그림과 같습니다. 나름 그럴싸한 결과를 얻은 것으로 보입니다.
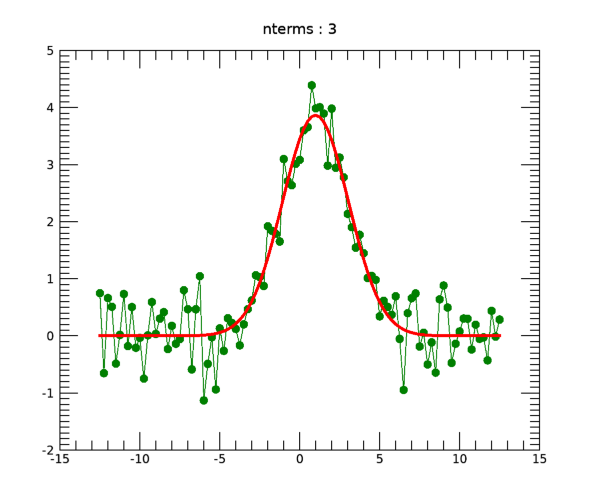
그리고 이렇게 근사된 Gaussian 함수에 대하여 FWHM(Full Width at Half Maximum)의 값도 계산할 수 있습니다. 여기서는 그 계산 방법은 다음과 같습니다.
fwhm = 2*SQRT(2*ALOG(2))*A[2]
PRINT, 'FWHM : ', fwhm
그리고 출력된 계산값은 다음과 같이 4.7 정도가 나왔는데, 위의 그림과 비교해보면 적절한 값이 산출된 것으로 보입니다.
FWHM : 4.70964
지금까지 3-term인 경우에 대한 결과를 얻어보았는데요. 이제 유사한 방식을 사용하여 4-term, 5-term, 6-term인 경우들에 대해서도 결과를 얻을 수 있습니다. 먼저 4-term인 경우를 보려면 위의 코드의 내용에서 일부만 수정하면 됩니다. 해당 부분들은 y를 정의했던 라인, PLOT 함수를 사용했던 라인, 그리고 GAUSSFIT 함수를 사용했던 라인들입니다. 그 내용은 다음과 같습니다.
y = 0.4*RANDOMN(seed, n)+a[0]*exp(-z^2/2)+a[3]
win = WINDOW(DIMENSIONS=[600, 500], /NO_TOOLBAR)
p1 = PLOT(x, y, SYMBOL='circle', /SYM_FILLED, COLOR='green', $
TITLE='nterms : 4', MARGIN=0.1, /CURRENT)
yfit = GAUSSFIT(x, y, coeff, NTERMS=4)
4-term인 경우는 베이스라인의 Y 위치만 변한 상태에 해당됩니다. 이러한 수정을 반영하여 전체적으로 다시 실행해보면 출력된 결과 및 그림은 다음과 같습니다.
Expect : 4.00000 1.00000 2.00000 1.00000 0.250000 0.0100000
Result : 3.82636 0.986438 2.02913 1.05432
FWHM : 4.70964

그리고 5-term인 경우는 베이스라인 자체가 1차 직선식이 되는 상태에 해당됩니다. 이 경우에 맞춰서 수정된 코드의 내용은 다음과 같습니다.
y = 0.4*RANDOMN(seed, n)+a[0]*exp(-z^2/2)+a[3]+a[4]*x
win = WINDOW(DIMENSIONS=[600, 500], /NO_TOOLBAR)
p1 = PLOT(x, y, SYMBOL='circle', /SYM_FILLED, COLOR='green', $
TITLE='nterms : 5', MARGIN=0.1, /CURRENT)
yfit = GAUSSFIT(x, y, coeff, NTERMS=5)
그리고 출력된 결과 및 그림은 다음과 같습니다.
Expect : 4.00000 1.00000 2.00000 1.00000 0.250000 0.0100000
Result : 3.82631 0.986327 2.02909 1.05434 0.250035
FWHM : 4.70964

마지막으로 6-term인 경우는 베이스라인 자체가 2차의 포물선 수식이 되는 상태에 해당됩니다. 이 경우에 맞춰서 수정된 코드의 내용은 다음과 같습니다.
y = 0.4*RANDOMN(seed, n)+a[0]*exp(-z^2/2)+a[3]+a[4]*x+a[5]*x^2
win = WINDOW(DIMENSIONS=[600, 500], /NO_TOOLBAR)
p1 = PLOT(x, y, SYMBOL='circle', /SYM_FILLED, COLOR='green', $
TITLE='nterms : 6', MARGIN=0.1, /CURRENT)
yfit = GAUSSFIT(x, y, coeff, NTERMS=6)
그리고 출력된 결과 및 그림은 다음과 같습니다.
Expect : 4.00000 1.00000 2.00000 1.00000 0.250000 0.0100000
Result : 3.95044 0.980025 2.11305 0.902628 0.249058 0.0117659
FWHM : 4.70964

이와 같이 X, Y 데이터 포인트들이 주어졌을 때 그 형태를 Gaussian 함수에 근사하려면, 위와 같은 요령으로 GAUSSFIT 함수를 사용하면 됩니다. IDL 도움말에서 GAUSSFIT 함수에 관한 내용을 살펴보면 부가적으로 사용 가능한 키워드들도 함께 소개되어 있습니다. 예를 들어 계수값들을 초기에 미리 가정하여 ESTIMATES 키워드를 통하여 설정할 수도 있고, 각 데이터 포인트에 대한 에러 편차를 MEASURE_ERRORS 키워드를 통하여 설정하는 등의 부가적인 설정들도 가능하다는 점을 함께 참조하시기 바랍니다.
'IDL > Math' 카테고리의 다른 글
| MEDIAN 함수에 의한 중간값 산출에 관한 유의사항 (0) | 2021.06.18 |
|---|---|
| GAUSS2DFIT 함수를 이용한 2차원 Gaussian 함수 근사 (0) | 2021.01.05 |
| 구면상의 지점 분포 데이터에 대한 격자화 및 유의사항 (0) | 2020.12.18 |
| NaN, Infinity와 FINITE 함수 (0) | 2020.08.10 |
| IDL에서 기초 통계량의 산출 및 유의사항 (한장강의 A/S) (0) | 2020.06.24 |