DG 체계에서 지도를 표출하고 그 위에 2차원 데이터를 중첩하는 방법에 관한 일련의 게시물들을 계속 올리고 있는데, 오늘은 3회차입니다. 앞서 1~2회차에서 소개된 내용은 2차원 데이터가 경도/위도 기반의 격자 분포를 하는 경우 DG 체계에서 지도상에 중첩 표출하는 방법이었습니다. 오늘은 또 다른 경우로서 바로 2차원 데이터가 거리 기반의 격자 분포를 하는 경우를 살펴보고자 합니다. 참고로 NG 체계에서 거리 기반의 격자 분포를 하는 2차원 데이터를 지도상에 중첩하는 방법 및 예제는 제가 전에도 관련 게시물들을 통하여 여러 차례 소개한 바 있습니다. 그런데 이러한 방식의 중첩 표출을 DG 체계에서 구현하려면 어떻게 해야 할까요? 물론 방법은 있습니다. 다만 이를 위해서는 제가 1회차 게시물의 서두에서 언급했던 "방법 2"를 사용해야 합니다. 즉 다음과 같은 방식입니다.
< 방법 2 >
MAP_PROJ_INIT 함수
PLOT 프로시저
MAP_CONTINENTS 프로시저
MAP_GRID 프로시저
참고로 방법 1에서는 지도를 처음에 셋업할 때 MAP_SET 프로시저를 사용했던 반면, 방법 2에서는 지도를 처음에 셋업할 때 MAP_SET 프로시저 대신 MAP_PROJ_INIT 함수를 사용하는 방법으로 가야한다는 것이 가장 중요합니다. 여기서 사용할 MAP_PROJ_INIT 함수는 지도의 투영법, 범위 등에 대한 설정을 하면 그 설정 데이터를 구조체(Structure)의 형태로 되돌려주는 역할을 합니다. 다만 이 함수 자체는 표출 기능이 없습니다. 그 대신 바로 이어서 PLOT 명령을 사용하여 지도의 기본 틀을 표출하고 그 이후에 MAP_CONTINENTS, MAP_GRID 등을 사용하여 지도를 완성해가는 방식입니다. 먼저 바탕 지도의 표출 과정부터 살펴보면 다음과 같습니다.
DEVICE, DECOMPOSED=0
WINDOW, XSIZE=600, YSIZE=600
!P.BACKGROUND = 255
limit = [25, 115, 45, 135]
m = MAP_PROJ_INIT('Lambert Conformal Conic', LIMIT=limit, $
CENTER_LONGITUDE=125, CENTER_LATITUDE=35, $
STANDARD_PAR1=30, STANDARD_PAR2=60)
HELP, m.uv_box
PRINT, m.uv_box
PLOT, m.uv_box[[0, 2]], m.uv_box[[1, 3]], $
XST=1, YST=1, XTICKLEN=1e-6, YTICKLEN=1e-6, $
XTICKFORMAT='(A1)', YTICKFORMAT='(A1)', $
XTITLE='LONGITUDE', YTITLE='LATITUDE', $
XMARGIN=[5, 5], YMARGIN=[3, 3], COLOR=0, /NODATA
바탕이 될 지도의 전반적인 특성은 앞서 1~2회차 게시물의 내용과 동일합니다. 다만 여기서는 MAP_PROJ_INIT 함수에서 지도의 투영법 및 범위 등을 설정하고 그 정보가 담긴 구조체(Structure)를 m이라는 이름으로 돌려받았습니다. 그리고 구조체 m이 담고 있는 여러 종류의 세부 정보들 중에서도 여기서는 uv_box라는 항목만 따로 추출하여 사용하게 됩니다. 구조체의 문법상 이 항목은 m.uv_box가 되고 HELP 및 PRINT에 의하여 출력된 이 항목에 관한 내용을 보면 다음과 같습니다.
<Expression> DOUBLE = Array[4]
-1032226.3 -1109769.9 1032226.3 1126221.5
이와 같이 4개의 실수값들로 구성되어 있고 각각의 값들은 위와 같습니다. 이 값들은 미터(m) 단위의 거리값들입니다. 앞서 MAP_PROJ_INIT 함수 내에서 지도의 중심이 될 지점의 경도/위도 좌표를 (125, 35)로 설정하였는데, 이 지점이 원점인 XY 좌표계를 가정하여 지도의 전체 범위를 거리 단위로 측정한 좌표값들이 바로 위의 4개의 값들이 됩니다. 즉 지도의 전체 범위에 대하여 좌측 하단 꼭지점의 거리 단위 좌표값이 (-1032226.3, -1109769.9)이고 우측 상단 꼭지점의 거리 단위 좌표값이 (1032226.3, 1126221.5)라는 의미입니다. 대략적으로는 가로 및 세로 방향으로 약 2100~2200km 정도라고 보면 됩니다. 그래서 바로 이어서 사용된 PLOT 명령은 이러한 정보를 활용하여 거리 좌표계 기반의 기본 틀을 표출하는 역할을 합니다. 일단 여기까지만 실행하게 되면 다음과 같이 사각형 박스만 표시됩니다.

따라서 대륙경계선 및 경위도 격자선의 표시를 위해서는 다음과 같이 MAP_CONTINENTS 및 MAP_GRID 명령을 추가적으로 사용해야 합니다.
MAP_CONTINENTS, MAP_STRUCTURE=m, COLOR=0, /HIRES, /COASTS
MAP_GRID, COLOR=0, LONDEL=5, LATDEL=5, BOX_AXES=0.1, MAP_STRUCTURE=m
여기서는 두 명령 모두 공통적으로 MAP_STRUCTURE 키워드에 m이 부여된 것에 주목해야 합니다. 이미 언급했듯이 m은 앞서 MAP_PROJ_INIT 함수로 돌려받은 지도 설정 데이터인데요. 이와 같이 MAP_PROJ_INIT 함수를 사용하여 지도 표출을 하는 작업에서는 그 함수로 돌려받은 설정 정보(여기서는 m)를 계속 활용해야 합니다. 어쨌든 이렇게 처리하면 표출 결과는 다음과 같습니다.

이제 이렇게 표출된 지도상에 2차원 데이터를 중첩하는 작업으로 진행합니다. 이를 위해서는 두가지 계산 작업이 선행되어야 합니다. 즉 중첩될 2차원 데이터가 커버하는 영역에 대한 위치 및 범위에 관한 정보를 계산해야 합니다. 구체적은 항목들은 다음과 같이 두가지입니다.
1) 2차원 데이터의 커버 영역의 좌측 하단 꼭지점의 위치 좌표 (거리 단위)
2) 2차원 데이터의 커버 영역의 가로 방향 및 세로 방향의 크기 (픽셀 단위)
먼저 1)에서 언급된 좌측 하단 꼭지점의 위치는 경도/위도 좌표로 (120, 30)이라고 가정하겠습니다. 그러면 이 좌표를 거리 기반 좌표로 환산해야 하는데 이러한 계산을 위해서는 MAP_PROJ_FORWARD 함수를 사용해야 한다는 것이 중요합니다. 그 과정은 다음과 같습니다.
lon0 = 120
lat0 = 30
tmp = MAP_PROJ_FORWARD(lon0, lat0, MAP_STRUCTURE=m)
HELP, tmp
PRINT, tmp
여기서는 MAP_PROJ_FORWARD 함수에 의하여 환산된 좌표 정보를 tmp라는 항목으로 얻어서 그 내용을 출력하도록 했는데, 출력된 결과를 보면 다음과 같습니다.
TMP DOUBLE = Array[2]
-482127.57 -534042.15
즉 경위도 좌표로 (120, 30)인 위치는 m 단위의 거리 좌표로는 (-482127.57, -534042.15)이 된다는 의미입니다. 이제 그 다음에는 2)에서 언급된 지도 커버 영역의 가로 및 세로 방향의 픽셀 단위 크기 정보를 계산해야 합니다. 이러한 계산을 위해서는 다음과 같이 CONVERT_COORD 함수를 사용합니다.
cv = CONVERT_COORD([tmp[0], tmp[0]+1400000], [tmp[1], tmp[1]+1400000], /DATA, /TO_DEVICE)
HELP, cv
PRINT, cv
여기서는 일단 2차원 데이터의 가로 및 세로 방향의 거리(m) 단위 크기를 각각 1400000m 즉 1400km인 것으로 가정하였습니다. 그리고 거리 단위의 좌표값을 픽셀 단위로 환산하는 과정이기 때문에 /DATA 및 /TO_DEVICE 키워드가 사용되었습니다. 출력된 결과를 보면 다음과 같습니다.
CV DOUBLE = Array[3, 2]
178.56338 173.40865 0.0000000
531.19924 500.24355 0.0000000
이것은 그래픽창에서 2차원 데이터 이미지의 위치 범위가 픽셀 단위로 가로 방향으로는 대략 179~531이고 세로 방향으로는 173~500이 된다는 의미입니다. 따라서 이러한 정보를 이용하면 2차원 데이터 이미지의 표출에 필요한 정보들을 다음과 같이 계산할 수 있습니다.
stx = ROUND(cv[0, 0])
sty = ROUND(cv[1, 0])
xsz = ROUND(cv[0, 1])-ROUND(cv[0, 0])+1
ysz = ROUND(cv[1, 1])-ROUND(cv[1, 0])+1
여기서는 이미지의 좌측 하단 꼭지점의 좌표 (stx, sty) 및 이미지의 가로 방향 크기 xsz, 세로 방향 크기 ysz를 모두 픽셀 단위로 얻은 것입니다. 이제 이러한 위치 정보들을 이용하여 이미지를 표출하면 됩니다. 이를 위해서는 다음과 같이 34번 컬러테이블을 적용하면서 TVSCL 명령을 사용합니다. 그 과정은 다음과 같습니다.
LOADCT, 34
TVSCL, data, stx, sty
LOADCT, 0
MAP_CONTINENTS, MAP_STRUCTURE=m, COLOR=0, /HIRES, /COASTS
MAP_GRID, COLOR=0, LONDEL=5, LATDEL=5, BOX_AXES=0.1, MAP_STRUCTURE=m
다만 여기서는 앞서 이미 사용했던 MAP_CONTINENTS, MAP_GRID가 또 등장하고 있습니다. 즉 이미지가 표출될 때 대륙경계선 및 격자선이 가려지지 않도록 하려면 표출의 순서를 이렇게 해야한다는 것을 유의하면 됩니다. 표출된 결과는 다음과 같습니다.
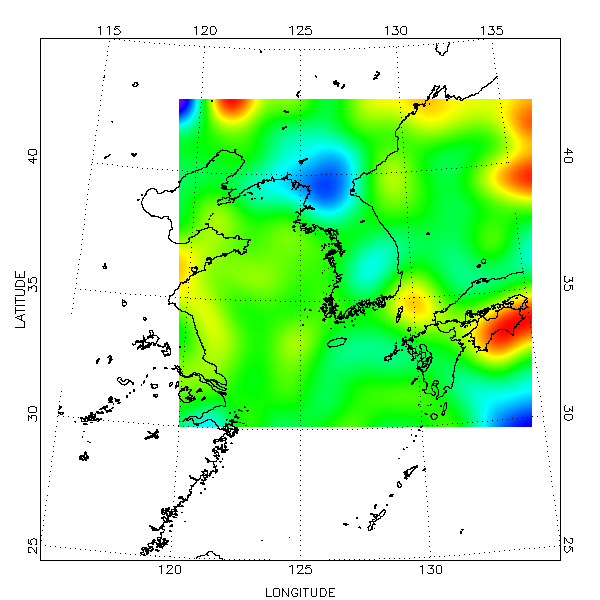
이와 같이 LCC 투영법 지도상에 거리 기반의 격자 분포를 하는 2차원 데이터를 중첩하는 과정을 DG 체계에서는 대략 이런 방식으로 처리할 수 있습니다. 물론 이 그림을 보면 보완이 필요한 부분들이 좀 보입니다. 특히 LCC 투영법이다보니 경위도 격자선이 비어있는 부분이 보이는 것도 그렇고, 이왕이면 컬러바도 함께 있으면 좋을 것 같습니다. 이러한 작업들은 다음 회차에서 계속 진행해보도록 하겠습니다.
'IDL > Direct Graphics' 카테고리의 다른 글
| DG 체계에서 지도와 이미지 중첩 표출 [4] (2) | 2023.09.25 |
|---|---|
| DG 체계에서 컬러바를 직접 제작하기 (2) | 2023.09.18 |
| DG 체계에서 지도와 이미지 중첩 표출 [2] (0) | 2023.09.05 |
| DG 체계에서 지도와 이미지 중첩 표출 [1] (0) | 2023.09.01 |
| LCC 투영법 기반의 지도 외곽 및 격자선 처리 (DG 체계) (2) | 2023.08.22 |