2차원 공간상에 흩뿌려진 지점(point)들이 있고 각 지점마다 물리량 값이 존재하는 형태의 데이터를 표출하는데 있어서는 아마도 NG 체계에서 SCATTERPLOT 함수를 사용하는 것이 가장 일반적이고 적절한 방법일 것 같습니다. 예를 들자면 다음과 같은 케이스입니다.
n = 10
x = RANDOMU(-1, n)*10
y = RANDOMU(-2, n)*10
val = RANDOMU(-4, n)*100
win = WINDOW(DIMENSIONS=[600, 600], /NO_TOOLBAR)
ct = COLORTABLE(74, /REVERSE)
sc = SCATTERPLOT(x, y, SYMBOL='circle', /SYM_FILLED, $
MAGNITUDE=BYTSCL(val, MIN=0, MAX=100), RGB_TABLE=ct, MARGIN=0.1, /CURRENT)
cb = COLORBAR(RGB_TABLE=ct, RANGE=[0, 100], POSITION=[0.2, 0.96, 0.8, 0.98])
이 내용은 2차원 공간상의 10개의 지점들로 구성된 데이터를 가상으로 생성하고 SCATTERPLOT 함수를 사용하여 XY 평면상에 표출하는 과정입니다. 지점들의 X, Y 좌표값은 각각 0~10의 범위 내에 존재하도록 하였고, 각 지점의 색상은 그 지점의 데이터 값을 0~100의 범위로 스케일링하여 지정된 컬러테이블 내에서 그 값에 맞춰서 해당 색상으로 나타나도록 하였습니다. 이를 위하여 SCATTERPLOT 함수의 MAGNITUDE 및 RGB_TABLE 속성이 사용되었습니다. 이 과정에 의하여 표출된 그림은 다음과 같습니다.

그런데 오늘은 여기서 그치지 않고 이러한 데이터를 3차원 공간상에서 막대의 형태로 가시화해보고자 합니다. 즉 각 지점에 막대가 위치하고 그 지점의 데이터 값이 막대의 길이로 대응되도록 하려는 의도입니다. 사실 2차원 공간상에서 막대그래프를 표출하는 기능을 담당하는 BARPLOT 함수가 이미 존재하긴 합니다. 하지만 3차원 공간에 해당되는 기능은 따로 제공되지는 않습니다. 물론 3차원 공간상에서 막대그래프를 표출하는 예제를 제가 예전에 관련 게시물을 통하여 한번 소개해드린 적은 있습니다. 다만 이 경우는 2차원 격자형 데이터에 한정하여 SURFACE 함수를 약간 응용한 제한적인 방법이라고 볼 수 있으며, 오늘 다루고자하는 불규칙하게 흩뿌려진 데이터에 대한 것은 또 다른 얘기입니다. 그러면 지금부터 이 "또 다른 얘기"를 시작해보도록 하겠습니다.
일단 데이터는 앞서 정의했던 x, y, val 배열들을 그대로 사용합니다. 그리고 XYZ 축으로 구성되는 3차원 공간을 정의하고 표출하는데 있어서는 PLOT3D 함수를 사용하면 됩니다. 그 과정의 시작은 다음과 같습니다.
win = WINDOW(DIMENSIONS=[600, 600], /NO_TOOLBAR)
p = PLOT3D(x, y, val, /NODATA, XRANGE=[0, 10], YRANGE=[0, 10], $
ZRANGE=[0, 100], CLIP=0, /CURRENT)
이와 같이 PLOT3D 함수에 x, y, val을 인수로 부여하되 /NODATA 키워드를 사용함으로써 데이터들이 실제로 표출되지는 않도록 하였습니다. 어차피 데이터 표출 과정은 나중에 따로 추가할 예정입니다. 그리고 각 축의 범위는 데이터의 특성을 그대로 반영하였습니다. 따라서 여기까지의 과정만 실행된 모습은 다음 그림과 같이 휑합니다.

이제부터 데이터에 맞는 가시화 요소들을 추가해야 하는데요. 두가지 방법을 제시하고자 합니다. 첫번째는 각 지점의 위치마다 데이터 값이 길이로 대응되는 선(Line)을 표시하는 방법입니다. 그 과정은 다음과 같습니다.
z_bot = p.ZRANGE[0]
FOR j = 0, n-1 DO BEGIN
px = [x[j], x[j]]
py = [y[j], y[j]]
pz = [z_bot, val[j]]
ln = POLYLINE(px, py, pz, THICK=3, COLOR='blue', /DATA)
ENDFOR
이와 같이 POLYLINE 함수를 사용하여 각 지점별 위치마다 해당 길이의 선을 표시하는 작업을 반복형 구문을 사용하여 처리하는 것입니다. 실제로 선의 길이에 해당되는 것이 여기서는 pz인데, Z축의 하한값인 z_bot로 시작하여 해당 지점의 데이터 값인 val[j]로 끝나는 선이 되는 효과를 얻게 됩니다. 결과를 보면 다음 그림과 같습니다.

이 그림을 보면 각 위치마다 그 데이터 값에 맞는 길이의 선이 표시되어 있는 것이 보입니다. 그리고 THICK 속성을 사용하여 선을 좀 두껍게 처리하였고 색상은 일괄적으로 파란색으로 처리하였습니다. 실제로 그림이 표출된 그래픽창에서 마우스 왼쪽 버튼을 플롯 상에서 클릭하여 드래그하여 돌려가면서 보면 더 구체적으로 확인이 됩니다. 그런데 여기서 한발 더 나아가서, 맨 처음에 SCATTERPLOT 함수로 표출할 때처럼 각 선의 색상이 데이터 값의 크기에 대응되도록 하는 것도 가능할까요? 물론 가능합니다. 다만 이를 위해서는 색상에 관한 추가적인 처리가 필요합니다. 그 과정은 다음과 같습니다. 바로 앞서 그래픽창을 띄웠던 처음 부분부터 다음의 내용으로 대체해야 합니다.
win = WINDOW(DIMENSIONS=[600, 600], /NO_TOOLBAR)
p = PLOT3D(x, y, val, /NODATA, XRANGE=[0, 10], YRANGE=[0, 10], $
ZRANGE=[0, 100], CLIP=0, /CURRENT)
ct = COLORTABLE(74, /REVERSE)
z_bot = p.ZRANGE[0]
FOR j = 0, n-1 DO BEGIN
px = [x[j], x[j]]
py = [y[j], y[j]]
pz = [z_bot, val[j]]
cv = BYTSCL(val[j], MIN=0, MAX=100)
clr = REFORM(ct[cv, *])
ln = POLYLINE(px, py, pz, THICK=3, COLOR=clr, /DATA)
ENDFOR
z_plane = POLYGON([p.XRANGE[0], p.XRANGE[1], p.XRANGE[1], p.XRANGE[0]], $
[p.YRANGE[0], p.YRANGE[0], p.YRANGE[1], p.YRANGE[1]], $
[p.ZRANGE[0], p.ZRANGE[0], p.ZRANGE[0], p.ZRANGE[0]], $
FILL_COLOR='light gray', /DATA)
cb = COLORBAR(RGB_TABLE=ct, RANGE=[0, 100], POSITION=[0.2, 0.90, 0.8, 0.94])
이 내용의 핵심적인 요소는 앞서 제시했던 것과 동일합니다. 다만 사용하고자 하는 컬러테이블을 COLORTABLE 함수로 정의하고, 반복형 구문 내에서는 BYTSCL 함수를 사용하여 각 데이터 값을 0~100의 범위 내의 컬러값으로 환산하여 이것이 선의 색상값으로 대응되도록 하는 부분이 추가되었습니다. 그 외에도 POLYGON 함수를 사용하여 Z축의 맨 하단에 연회색 평면 폴리곤을 추가하여 바닥면을 나타내보았습니다. 이게 없으면 그림 내에서 막대들이 너무 붕 떠있는 듯한 감이 있기 때문입니다. 또한 COLORBAR 함수를 사용하여 컬러바도 함께 표시하였습니다. 표출 결과를 보면 다음 그림과 같습니다.

이와 같이 각 지점의 데이터 값의 크기가 선의 길이 뿐 아니라 색상으로도 대응된 결과를 얻을 수 있습니다. 맨 처음에 SCATTERPLOT 함수로 표출했던 그림과 비교해보면 색상이 정확히 대응되었음을 확인할 수 있습니다. 역시 이 그림도 마우스 드래그로 이리저리 돌려보면서 확인해보는 것이 좋습니다. 어쨌든 3차원 공간상에서 선의 형태로 표출하는 방식은 대략 이와 같습니다.
그런데 이와 같이 선의 형태로 표시하는 것만으로는 뭔가 좀 부족합니다. 선 대신 아예 육면체 형태의 막대로 표시할 수 있다면 좀 더 그럴싸한 그림이 될 것 같습니다. 그런데 이러한 처리가 가능할까요? 역시 가능은 합니다. 다만 이 방법은 좀 더 복잡합니다. 그 이유는 각 지점마다 표시될 막대를 육면체 폴리곤(Polygon)의 형태로 구현해야 하기 때문입니다. 그리고 이러한 육면체 폴리곤을 비교적 쉽게 구현하기 위해서는 MESH_OBJ 명령을 사용하는 것이 필요합니다. 즉 MESH_OBJ 명령을 사용하여 육면체 폴리곤을 구현하는 방법을 알아야 한다는 얘기입니다. 일단 전체적인 과정부터 보면 다음과 같습니다.
win = WINDOW(DIMENSIONS=[600, 600], /NO_TOOLBAR)
p = PLOT3D(x, y, val, /NODATA, XRANGE=[0, 10], YRANGE=[0, 10], $
ZRANGE=[0, 100], CLIP=0, /CURRENT)
ct = COLORTABLE(74, /REVERSE)
z_bot = 0; lower Z value
th = 0.15
FOR j = 0, n-1 DO BEGIN
arr = [[-th, th, th, -th, -th], [-th, -th, th, th, -th], [0, 0, 0, 0, 0]]
arr = TRANSPOSE(arr)
MESH_OBJ, 5, vertices, polygons, arr, P2=[z_bot, z_bot, val[j]]
polygons = [polygons, 4, 0, 1, 2, 3, 4, 5, 6, 7, 8]
xv = REFORM(vertices[0, *])+x[j]
yv = REFORM(vertices[1, *])+y[j]
zv = REFORM(vertices[2, *])
cv = BYTSCL(val[j], MIN=0, MAX=100)
clr = REFORM(ct[cv, *])
pol = POLYGON(xv, yv, zv, CONNECTIVITY=polygons, $
FILL_COLOR=clr, COLOR=clr, CLIP=0, /DATA)
ENDFOR
z_plane = POLYGON([p.XRANGE[0], p.XRANGE[1], p.XRANGE[1], p.XRANGE[0]], $
[p.YRANGE[0], p.YRANGE[0], p.YRANGE[1], p.YRANGE[1]], $
[p.ZRANGE[0], p.ZRANGE[0], p.ZRANGE[0], p.ZRANGE[0]], $
FILL_COLOR='light gray', /DATA)
cb = COLORBAR(RGB_TABLE=ct, RANGE=[0, 100], POSITION=[0.2, 0.90, 0.8, 0.94])
아무래도 앞서 했던 작업보다는 좀 더 복잡합니다. 특히 FOR 구문 내에서 MESH_OBJ 명령이 사용된 부분이 더 그러한데요. 일단 그 취지는 각 지점마다 Z축의 바닥값인 z_bot으로 시작하여 데이터 값인 val[j]로 끝나는 육면체 막대 폴리곤을 일일이 구현하는 것입니다. 이 때 육면체의 가로 및 세로 방향 두께는 2*th가 되도록 하였습니다. 그리고 MESH_OBJ 명령을 실행하여 얻은 vertices 및 polygons는 육면체를 구성할 점(vertex)들의 좌표 및 연결성(connectivity) 정보에 해당됩니다. 이 정보들을 나중에 POLYGON 함수에 투입하여 육면체 폴리곤을 생성하게 된다고 보시면 됩니다. 사실 MESH_OBJ 명령의 사용법이 꽤 복잡한 편이기 때문에 여기서는 이와 관련된 긴 설명은 생략하겠습니다. 어쨌든 결과로 얻게 되는 그림은 다음과 같습니다.
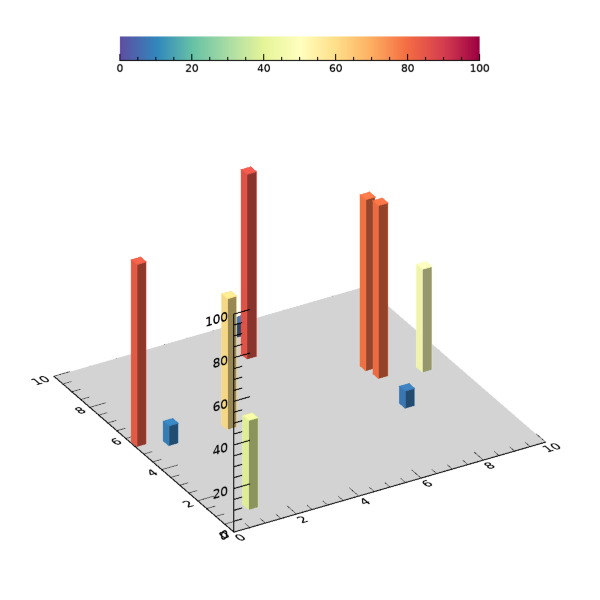
이와 같이 각 지점의 데이터가 육면체 막대로 표시되고 데이터 값이 길이와 색상으로 반영된 모습을 볼 수 있습니다. 그리고 경우에 따라서는 육면체 막대의 모서리 윤곽선만 다른 색으로 설정할 수도 있는데, 반복형 구문 내에서 POLYGON 함수가 사용된 부분의 COLOR 속성만 다음과 같이 별도의 색상으로 설정하면 됩니다.
FOR j = 0, n-1 DO BEGIN
~~~~~~~~
pol = POLYGON(xv, yv, zv, CONNECTIVITY=polygons, $
FILL_COLOR=clr, COLOR='black', CLIP=0, /DATA)
ENDFOR
그러면 다음과 같은 그림을 얻게 됩니다.
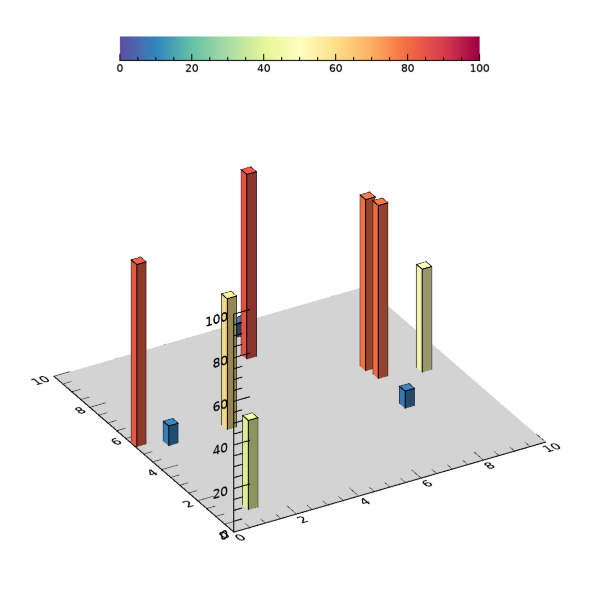
그리고 변수 th의 값을 좀 더 크게 하면 더 두꺼운 막대로 표시하는 것도 가능합니다. 예를 들어 이 값을 0.15 대신 0.3으로 설정하면 결과는 다음 그림과 같습니다.
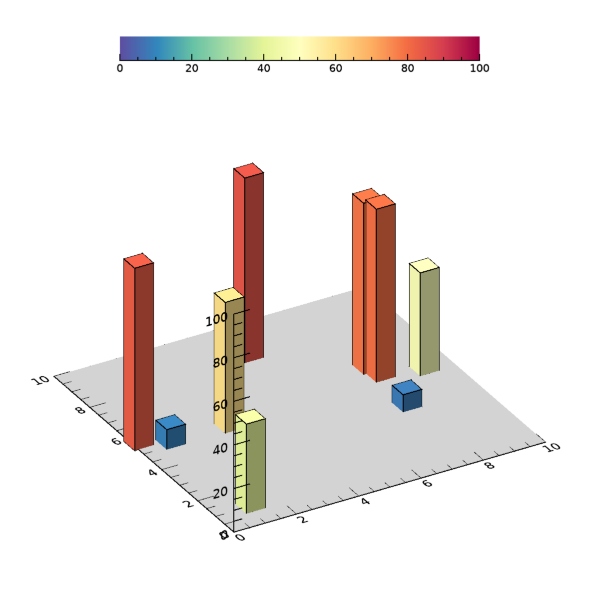
이와 같은 방법을 사용하면 불규칙하게 흩뿌려진 데이터 포인트들에 대하여 그 값에 대응하는 길이의 막대들을 표시할 수 있습니다. 다만 앞서 설명했듯이 이 방법에서는 각 포인트마다 육면체 폴리곤을 일일이 구현하여 표시하기 때문에 데이터 포인트들의 갯수가 많아질 경우에는 그림이 더 복잡해지고 구현에 약간의 시간이 소요될 수도 있습니다. 예를 들어 10개가 아닌 100개로(n=100) 설정하여 처리를 해보면 그 모습은 다음 그림과 같은데, 이 결과를 얻는데 제가 연식이 좀 되는 PC에서 테스트해본 바로는 약 10초 정도가 걸렸습니다. 물론 이것은 컴퓨터의 사양에 따라서 얼마든지 달라질 수 있습니다. 참고해두시면 좋을 것 같습니다.

'IDL > New Graphics' 카테고리의 다른 글
| SetData 메서드의 활용 예제 [2] (0) | 2022.06.30 |
|---|---|
| 구간이 불규칙한 불연속 컬러테이블 기반의 표출 (0) | 2022.06.24 |
| SetData 메서드의 활용 예제 [1] (0) | 2022.05.25 |
| _EXTRA 키워드의 활용 예제 (0) | 2022.04.28 |
| 컬러테이블만 표출하는 방법 (0) | 2022.04.19 |