얼마전에 라돈 변환(Radon Transform) 기법을 IDL에서 사용하는 방법에 관한 게시물을 올린 바 있는데요. 오늘은 약간 비슷한 것 같으면서도 좀 다른 또 다른 기법인 허프 변환(Hough Transform)이라는 기법을 IDL에서 사용하는 방법에 관하여 예제와 함께 소개해보고자 합니다. 허프 변환 기법은 2차원 이미지 상에서 직선(Straight Line)의 모습을 갖는 형체들을 탐지하는 작업에 주로 사용됩니다. 기본적으로는 공간 도메인(Spatial Domain)에 존재하는 2차원 이미지를 허프 도메인(Hough Domain)으로 변환하게 되는데, 이 과정에서는 먼저 2차원 이미지 내에서 화소값이 0이 아닌 화소들을 모두 점(Point)으로 간주합니다. 만약 이미지 내에서 이러한 점들을 지나가는 직선의 형체가 존재한다고 하면, 허프 도메인에서는 그러한 직선들을 찾아낼 수 있게 됩니다. 물론 허프 도메인으로부터 공간 도메인으로의 역변환(Backprojection)도 가능합니다. IDL에서는 HOUGH 함수를 사용하여 이러한 작업들을 수행할 수 있는데, IDL 도움말에서 HOUGH 함수에 관한 내용을 찾아보면 기본 원리에 관한 설명도 볼 수 있습니다. 일단 도움말에 있는 그림을 보면 다음과 같습니다.

이와 같이 공간 도메인 상에서 (x, y) 좌표로 존재하는 포인트를 허프 도메인 상에서 (각도, 거리) 좌표로 변환한다는 점에서는 지난번에 소개한 라돈 변환의 경우와 유사한 측면이 있습니다. 다만 허프 변환의 경우에서는, 원래 공간 도메인 상에서 일직선상에 존재하는 여러 포인트들이 있을 경우 허프 도메인 상에서는 사인(Sine) 형태의 곡선들이 교차하는 부분으로 반영됩니다. 따라서 공간 도메인에서 일직선 상에 존재하는 포인트들이 많을수록 허프 도메인 상에서는 한 지점에서 다수의 곡선들이 교차하게 되고, 이러한 부분들을 추출하면 공간 도메인 상에서 존재하는 직선의 패턴을 인식할 수 있게 됩니다. 제가 대략적으로만 설명을 드렸지만, 허프 변환의 원리에 관한 더 자세한 내용이 궁금하시다면 IDL 도움말 또는 웹상에서의 관련 검색을 통하여 직접 확인해보시길 권장합니다.
그러면 IDL에서 허프 변환 기법을 적용하는 간단한 예제를 살펴보기로 하겠습니다. 이해를 돕기 위하여 다음과 같이 가상의 2차원 이미지 데이터를 생성합니다.
img = INTARR(400, 400)
img[99, 349] = 1
img[199, 249] = 1
img[299, 149] = 1
img[229, 159] = 1
HELP, img
PRINT, MIN(img), MAX(img)
sz = SIZE(img, /DIM)
여기서는 400x400의 형태를 갖는 정수형 값들로 구성된 2차원 배열을 생성하였습니다. 그리고 처음에는 배열 내 모든 값들을 0으로 통일했지만 그 중 4개의 포인트들에 대해서만 값을 1로 설정하였습니다. 이제 다음과 같은 과정에 의하여 이 데이터의 모습을 표출해봅시다.
win1 = WINDOW(DIMENSIONS=sz, /NO_TOOLBAR)
im1 = IMAGE(img, MARGIN=0, /CURRENT)
그 모습은 다음 그림과 같습니다.

이와 같이 예제로 사용할 2차원 이미지 내에는 4개의 점들이 존재합니다. 사실 화면상으로는 점들이 너무 작아서 잘 안보일 수도 있기 때문에 여러분들이 직접 실행을 해서 화면에서 직접 확인해보시길 권합니다. 위의 그림에서 4개의 점들의 위치를 명확하게 표시해본 모습은 다음과 같습니다.

어쨌든 이 4개의 점들 중에는 일직선 상에 존재하는 경우들이 분명히 존재합니다. 눈으로만 봐도 판단할 수 있듯이, 3개의 점들로 이어지는 직선도 있고 2개의 점들로만 이어지는 직선들도 있습니다. 이러한 정보를 허프 변환에 의하여 명시적으로 확인할 수 있게 됩니다. 허프 변환의 적용을 위해서는 다음과 같이 HOUGH 함수를 사용하면 됩니다.
result = HOUGH(img, RHO=rho, THETA=theta)
HELP, result
PRINT, MIN(result), MAX(result)
HOUGH 함수의 사용 방법은 RADON 함수와 상당히 유사합니다. RHO와 THETA 키워드를 통하여 거리 및 각도 값들로 구성된 배열들을 받아올 수 있다는 점도 동일합니다. 물론 변환의 결과 자체는 여기서는 result라는 배열로 받아왔는데, HELP 및 PRINT 명령에 의하여 출력된 내용을 보면 다음과 같습니다.
RESULT FLOAT = Array[887, 567]
0.00000 3.00000
여기서 최대값이 3이라는 것에 주목해야 하는데요. 이것은 원래의 공간 도메인 이미지 상에서 최대 3개의 점들이 지나가는 직선 형체가 존재한다는 뜻입니다. 물론 2개를 지나가는 직선들도 있고 1개만 지나가는 직선들도 존재할 것입니다. 그러면 이 result의 모습을 다음과 같이 표출해서 봅시다.
win2 = WINDOW(DIMENSIONS=[600, 500], /NO_TOOLBAR)
im2 = IMAGE(result, theta, rho, AXIS_STYLE=2, $
XTITLE='theta (radian)', YTITLE='R', $
ASPECT_RATIO=0, MARGIN=0.1, FONT_SIZE=10, /CURRENT)
그 모습은 다음 그림과 같습니다.

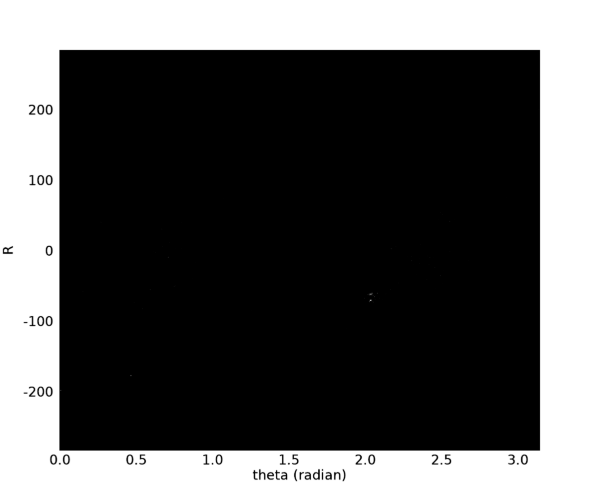
이것이 바로 허프 도메인으로 나타나는 허프 변환의 결과입니다. 이 그림에서는 곡선들이 서로 교차하는 지점들을 주로 주목하면 됩니다. 사실 이 그림에서도 곡선 및 교차점들이 또렷하게 보이는 편은 아니기 때문에 다음과 같이 교차점들만 표시해보았습니다.

왼쪽 부분에 곡선 3개가 교차하는 지점(붉은색 원으로 표시)이 보이는데 바로 이 지점에서의 값이 3이 됩니다. 그리고 곡선 2개가 교차하는 지점들(노란색 원으로 표시)도 3개가 보입니다. 이제 result를 사용하여 역변환(Backprojection)을 해봐야 할텐데요. 역변환을 하기 전에 result에 대하여 클리핑(Clipping) 처리를 한번 해주는 것이 좋습니다. 어차피 직선 형태의 패턴을 추출하는 것이 목적이고, 라돈 도메인 상에서는 직선에 해당되는 교차점들은 아무래도 화소값이 상대적으로 높기 때문에 클리핑 처리로 걸러내는 것이 가능하기 때문입다. 일단 다음과 같은 처리를 한번 해봅시다.
result = (result-1) > 0
이러한 처리를 해주면 result 배열 내에서 1보다 작았던 값들이 모두 0으로 처리되면서 그 정보가 사실상 사라지게 됩니다. 어차피 점 하나만 지나가는 직선들은 우리의 관심 대상이 아니기 때문입니다. 결국 이러한 처리를 해준다는 것은, 적어도 2개 이상의 점들을 지나는 직선들만 관심에 두겠다는 의미가 됩니다. 이렇게 클리핑 처리가 된 result를 다음과 같이 다시 한번 표출해보면 그 모습은 다음 그림과 같습니다.
win3 = WINDOW(DIMENSIONS=[600, 500], /NO_TOOLBAR)
im3 = IMAGE(result, theta, rho, AXIS_STYLE=2, $
XTITLE='theta (radian)', YTITLE='R', $
ASPECT_RATIO=0, MARGIN=0.1, FONT_SIZE=10, /CURRENT)

이와 같이 곡선의 형체들은 사라지고 점들만 남은 것을 볼 수 있습니다. 이 점들이 바로 원래의 공간 도메인 이미지 상에서 2개 이상의 점들이 지나가는 직선들에 해당됩니다. 역시나 이 그림에서도 교차점들이 잘 안보여서 다음과 같이 다시 표시해보았습니다.

이 모습을 잘 보면 곡선 2개가 교차되는 교차점들(노란색 원으로 표시)이 원래 3개였다가 여기서는 2개만 남은 것을 확인할 수 있습니다. 사라진 1개의 교차점은 원래의 이미지 상에서는 2개의 점이 지나는 직선 3개들 중 점 사이의 거리가 가장 먼 케이스에 해당됩니다. 이러한 형체는 별로 중요하지 않고 허프 도메인 상에서도 그리 또렷하게 보이는 편은 아니었기 때문에 이와 같이 걸러졌다고 보면 됩니다. 이제 이렇게 클리핑 처리까지 거친 result에 대하여 다음과 같이 역변환(Backprojection) 처리를 해주면 됩니다.
backproject = HOUGH(result, /BACKPROJECT, RHO=rho, THETA=theta, $
NX=sz[0], NY=sz[1])
HELP, backproject
PRINT, MIN(backproject), MAX(backproject)
역변환을 할 때에는 이와 같이 HOUGH 함수를 /BACKPROJECT 키워드와 함께 사용하면 됩니다. 역변환의 결과로 얻어진 backproject라는 배열을 다음과 같은 과정에 의하여 표출해봅시다.
win4 = WINDOW(DIMENSIONS=sz, /NO_TOOLBAR)
im4 = IMAGE(backproject, MARGIN=0, /CURRENT)
그 모습은 다음 그림과 같습니다.

이 모습을 보면 원래의 2차원 이미지 데이터 내에 존재하는 직선 형태의 패턴들만 추출되었음을 확인할 수 있습니다. 물론 여기서는 2개 이상의 점들을 지나는 직선들이 모두 확인된 상태입니다. 만약 3개의 점들이 지나는 직선들만 추출하고자 한다면, 앞서 result 배열에 대한 클리핑 처리 과정을 다음과 같이 바꿔주면 됩니다.
result = (result-2) > 0
이렇게 한 다음에 역변환 처리를 해주면 그 결과는 다음 그림과 같습니다.

이와 같이 3개의 점들을 지나는 직선 하나만 추출된 것을 확인할 수 있습니다. 그래서 매우 간단한 예제이긴 하지만, 아마 이 예제를 통하여 허프 변환의 원리와 효과에 대하여 어느 정도 설명이 되었으리라 생각합니다. 물론 더 복잡하고 실제에 가까운 데이터들을 사용해볼 수도 있습니다. 두번째 케이스로 사용해볼 예제 데이터 역시 다음과 같이 가상으로 생성해봅시다.
img = FIX(RANDOMU(seed, 400, 400) GT 0.95)
x = INDGEN(100)*4
img[x,0.5*x+20] = 1
img[x,0.5*x+30] = 1
img[-0.5*x+100,x] = 1
어차피 데이터만 다를 뿐 처리 과정은 앞서 제시된 예제 코드의 내용을 그대로 사용하면 됩니다. 일단 이 원본 2차원 데이터가 표출된 모습은 다음과 같습니다.

이 데이터의 경우 점들이 훨씬 많고 어지럽게 분포해 있습니다. 그런데 이 안에서도 어렴풋하게 직선과 같은 형체는 보입니다. 일단 이 데이터에 대하여 허프 변환을 적용하여 그 결과인 result 배열을 표출해본 모습은 다음과 같습니다.

원본 이미지 내에 점들이 워낙 많기 때문에 허프 변환의 결과도 이와 같이 복잡하게 나타납니다. 그런데 이 안에서 몇몇 밝게 보이는 부분들이 있습니다. 이러한 부분들이 바로 원본 이미지 내에서 많은 점들로 구성된 직선 형체들에 해당됩니다. 따라서 직선에 해당되는 부분들만 추출하기 위하여 이번에도 result 배열에 대한 클리핑 처리가 필요합니다. 다만 이번에는 result 배열 내 값들이 앞선 예제에서와는 다르기 때문에 다음과 같이 약 40 정도의 값을 사용하는 것이 좋을 것 같습니다.
result = (result-40) > 0
이렇게 클리핑 처리가 된 result 배열의 모습은 다음과 같습니다.
이와 같이 우측 하단 부분에서 밝게 보이는 두 개의 점들만 걸러진 상태가 됩니다. 그리고 이 상태에서 역변환을 한 결과는 다음과 같습니다.

그러면 이와 같이 원본 이미지 상에서 가장 두드러지게 나타났던 직선의 형체들만 검출된 것을 확인할 수 있습니다. 물론 이외에도 다른 예제들도 많이 있습니다. 관련 링크 하나를 아래에 첨부합니다.
이 링크의 웹페이지를 보면 HOUGH 및 RADON 함수를 이용하는 여러가지 예제들이 소개되어 있으므로 참고해두시면 좋을 것 같습니다. 제가 알기로는 자율주행 차량이 도로의 차선을 인식하는 것과 같은 작업에서 기본적으로 이러한 허프 변환 기법이 응용되는 것으로 알고 있습니다.
이번에 2회에 걸쳐서 IDL에서 라돈 변환(Radon Transform)과 허프 변환(Hough Transform) 기법들을 적용하는 방법 및 관련 예제들을 정리해보았는데요. 사실 여기서 소개한 예제들은 이러한 변환 기법들의 원리 설명을 위하여 어느 정도 단순화된 가상의 이미지 데이터들을 사용한 것입니다. 실전 이미지 데이터들은 이보다 더 복잡한 경우가 대부분이기 때문에, 그러한 이미지들에 대하여 바로 라돈이나 허프 변환을 적용한다고 해서 만족스러운 결과가 곧바로 나오지는 않을 가능성이 큽니다. 즉 전처리(Pre-Processing) 또는 후처리(Post-Processing) 과정들을 어느 정도 동반하면서 이러한 변환 기법들을 적용해야 하는 경우들도 많습니다. 물론 전처리나 후처리의 과정이 구체적으로 어떻게 진행되어야 하는가에 대해서는 따로 정해진 정답은 없습니다. 아무래도 데이터의 특성이나 분석 목적에 따라 다양한 경우들이 존재할 수 밖에 없을 것입니다. 위에 소개한 링크의 내용들에서도 아마 이러한 부분에 대한 짐작이 어느 정도 가능하리라 생각합니다.
'IDL > Image Processing' 카테고리의 다른 글
| 클리핑(Clipping) 기법의 이해와 응용 (0) | 2021.05.26 |
|---|---|
| 마스킹(Masking) 기법의 이해와 응용 (0) | 2021.05.17 |
| IDL에서의 라돈 변환(Radon Transform) 사용법 (0) | 2021.04.07 |
| Histogram Equalization 기법에 관하여 (0) | 2021.01.11 |
| 불규칙 격자 2차원 데이터의 이미지 표출에 관하여 [2] (0) | 2018.12.04 |