지난 회에서는 배열 합치기(Array Concatenation) 즉 배열과 배열을 합쳐서 더 큰 배열을 만드는 기법에 관하여 1차원 및 2차원 배열에 대한 방법들을 소개하였습니다. 오늘은 3차원 배열에 대한 방법을 소개해보고자 합니다. 아무래도 배열의 차원이 높아질수록 그 문법이 좀 더 복잡해지긴 합니다. 그러면 먼저 다음과 같이 4x5x3의 구조를 갖는 3차원 배열 a를 가정해봅시다.
a = FIX(RANDOMU(-1, 4, 5, 3)*50)
HELP, a
PRINT, a
이러한 3차원 배열은 그 세부값들을 출력해보면 다음과 같이 각각의 층(XY 평면)별로 나타납니다.
4 5 45 28
39 26 39 38
0 14 48 25
29 34 7 34
45 8 27 32
49 41 20 38
16 23 9 14
46 19 41 24
44 45 24 15
10 31 49 39
12 32 30 18
38 49 29 49
1 9 30 24
25 13 43 10
5 41 21 32
그런데 이왕이면 도식적으로 보면 더 좋을 것 같습니다. 그 모습은 다음 그림과 같습니다.
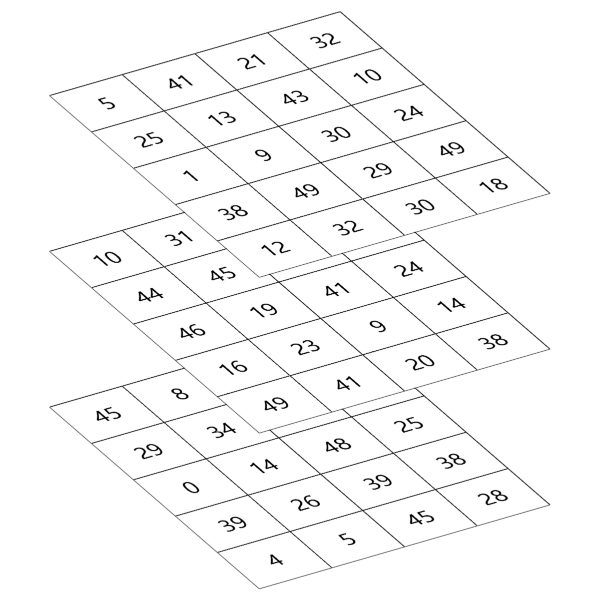
어쨌든 이렇게 정의된 배열 a가 있는 상태에서 또 다른 배열 b를 정의하여 둘을 합치는 방법을 살펴보겠습니다. 각 차원별로 총 세가지 케이스들이 있습니다. 각각의 케이스별로 차례로 살펴보도록 하겠습니다.
<1> 첫번째 차원 즉 X축 방향으로 배열 합치기
먼저 배열 b가 다음과 같이 2x5x3의 구조를 갖도록 정의해봅시다.
b = FIX(RANDOMU(-2, 2, 5, 3)*50)
HELP, b
PRINT, b
이렇게 정의된 배열 b의 모습은 출력된 내용을 통해서도 확인할 수 있겠지만 도식적으로 보면 다음 그림과 같습니다.
그러면 4x5x3인 배열 a와 2x5x3인 배열 b를 합쳐서 6x5x3의 배열 c를 얻는 과정이 됩니다. 이것은 첫번째 차원인 X 방향으로 크기가 늘어나는 경우인데요. 이렇게 하려면 두번째 및 세번째 차원의 크기가 서로 동일해야 한다는 것을 반드시 유의해야 합니다. 결과를 얻기에 앞서서 이 과정을 도식적으로 본다면 다음 그림과 같습니다.

위 그림에서는 이해를 돕기 위하여 합치기가 수행되는 방향을 붉은 선으로 표시해놓았습니다. 이제 실제로 이러한 결과를 얻는 과정은 다음과 같은 문법으로 처리해야 합니다.
c = [a, b]
HELP, c
PRINT, c
이 과정에 의하여 실제로 출력된 배열 c의 값들을 확인해보면 위의 그림과 같은 배열 합치기 작업이 제대로 수행되었음을 알 수 있을 것입니다.
C INT = Array[6, 5, 3]
4 5 45 28 26 5
39 26 39 38 26 47
0 14 48 25 27 41
29 34 7 34 30 18
45 8 27 32 28 25
49 41 20 38 39 12
16 23 9 14 40 45
46 19 41 24 16 43
44 45 24 15 3 28
10 31 49 39 38 9
12 32 30 18 2 37
38 49 29 49 35 36
1 9 30 24 43 0
25 13 43 10 24 46
5 41 21 32 24 39
<2> 두번째 차원 즉 Y축 방향으로 배열 합치기
이번에는 두번째 차원인 Y 방향으로 크기가 늘어나도록 합치는 경우를 봅시다. 이렇게 하려면 첫번째 및 세번째 차원의 크기가 서로 동일해야 한다는 것을 반드시 유의해야 합니다. 배열 a는 앞서 정의했던 그대로 4x5x3의 구조를 갖습니다. 따라서 배열 b는 다음과 같이 4x2x3의 구조로 정의해봅시다.
b = FIX(RANDOMU(-2, 4, 2, 3)*50)
HELP, b
PRINT, b
이렇게 정의된 배열 b의 모습은 출력된 내용을 통해서도 확인할 수 있겠지만 도식적으로 보면 다음 그림과 같습니다.

그러면 4x5x3인 배열 a와 4x2x3인 배열 b를 합쳐서 4x7x3의 배열 c를 얻는 과정이 됩니다. 결과를 얻기에 앞서서 이 과정을 도식적으로 본다면 다음 그림과 같습니다.

위 그림에서도 이해를 돕기 위하여 합치기가 수행되는 방향을 붉은 선으로 표시해놓았습니다. 이제 실제로 이러한 결과를 얻는 과정은 다음과 같은 문법으로 처리해야 합니다.
c = [[a], [b]]
HELP, c
PRINT, c
앞서 첫번째 차원인 X 방향으로 합치기를 했던 경우와 비교해보면, a와 b 각각에 대하여 꺽쇠괄호가 추가되었다는 차이가 있음을 유의하면 됩니다. 이 과정에 의하여 실제로 출력된 배열 c의 값들을 확인해보면 위의 그림과 같은 배열 합치기 작업이 제대로 수행되었음을 알 수 있을 것입니다.
C INT = Array[4, 7, 3]
4 5 45 28
39 26 39 38
0 14 48 25
29 34 7 34
45 8 27 32
26 5 26 47
27 41 30 18
49 41 20 38
16 23 9 14
46 19 41 24
44 45 24 15
10 31 49 39
28 25 39 12
40 45 16 43
12 32 30 18
38 49 29 49
1 9 30 24
25 13 43 10
5 41 21 32
3 28 38 9
2 37 35 36
<3> 세번째 차원 즉 Z축 방향으로 배열 합치기
이번에는 세번째 차원인 Z 방향으로 크기가 늘어나도록 합치는 경우를 봅시다. 이렇게 하려면 첫번째 및 두번째 차원의 크기가 서로 동일해야 한다는 것을 반드시 유의해야 합니다. 배열 a는 앞서 정의했던 그대로 4x5x3의 구조를 갖습니다. 따라서 배열 b는 다음과 같이 4x5x2의 구조로 정의해봅시다.
b = FIX(RANDOMU(-2, 4, 5, 2)*50)
HELP, b
PRINT, b
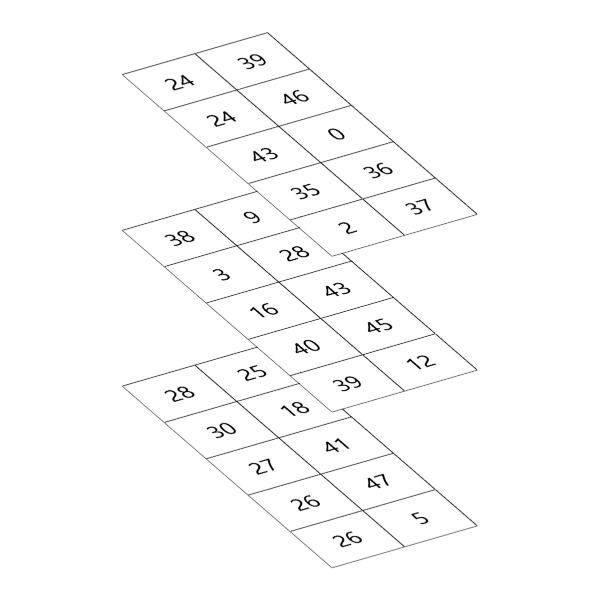
이렇게 정의된 배열 b의 모습은 출력된 내용을 통해서도 확인할 수 있겠지만 도식적으로 보면 다음 그림과 같습니다.

그러면 4x5x3인 배열 a와 4x5x2인 배열 b를 합쳐서 4x5x5의 배열 c를 얻는 과정이 됩니다. 결과를 얻기에 앞서서 이 과정을 도식적으로 본다면 다음 그림과 같습니다.
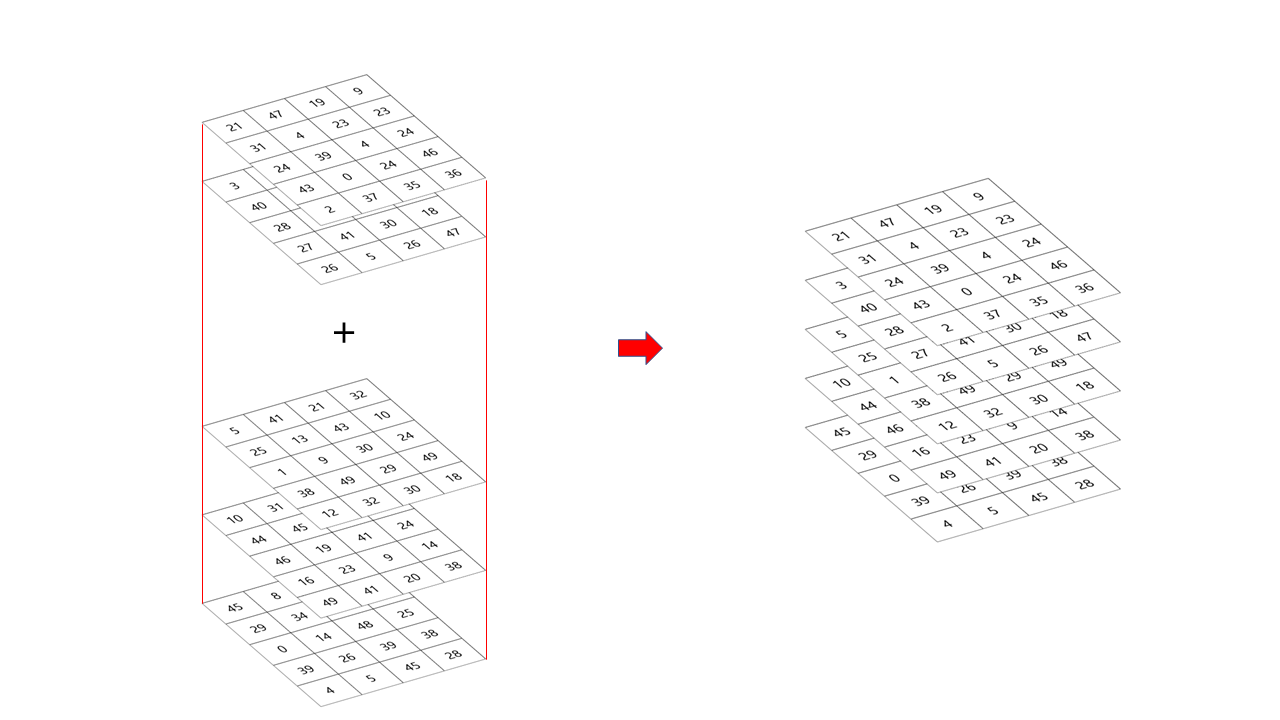
위 그림에서도 이해를 돕기 위하여 합치기가 수행되는 방향을 붉은 선으로 표시해놓았습니다. 이제 실제로 이러한 결과를 얻는 과정은 다음과 같은 문법으로 처리해야 합니다.
c = [[[a]], [[b]]]
HELP, c
PRINT, c
앞서 두번째 차원인 Y 방향으로 합치기를 했던 경우와 비교해보면, a와 b 각각에 대하여 꺽쇠괄호가 또 추가되었다는 차이가 있음을 유의하면 됩니다. 이 과정에 의하여 실제로 출력된 배열 c의 값들을 확인해보면 위의 그림과 같은 배열 합치기 작업이 제대로 수행되었음을 알 수 있을 것입니다.
C INT = Array[4, 5, 5]
4 5 45 28
39 26 39 38
0 14 48 25
29 34 7 34
45 8 27 32
49 41 20 38
16 23 9 14
46 19 41 24
44 45 24 15
10 31 49 39
12 32 30 18
38 49 29 49
1 9 30 24
25 13 43 10
5 41 21 32
26 5 26 47
27 41 30 18
28 25 39 12
40 45 16 43
3 28 38 9
2 37 35 36
43 0 24 46
24 39 4 24
31 4 23 23
21 47 19 9
이와 같이 3차원 배열들에 대한 배열 합치기(Array Concatenation)도 근본적인 원리는 2차원 배열의 경우와 거의 동일합니다. 다만 차원이 하나 더 있다는 것과 각 차원별로 적합한 문법을 적용해야 한다는 것만 유의하면 됩니다.
'IDL > 배열 생성 및 처리' 카테고리의 다른 글
| 원소값들을 직접 표기하여 배열을 생성하는 법 (3차원까지) (0) | 2023.11.29 |
|---|---|
| 배열 내 값들에 대한 샘플링(Sampling) (4) | 2023.05.26 |
| 배열 합치기(Array Concatenation) [1] (0) | 2023.04.11 |
| INDGEN 함수 사용시 주의할 점 (0) | 2023.02.16 |
| 배열 처리 함수 소개 (SHIFT, REVERSE, ROTATE) [2] (0) | 2022.04.06 |