MESH_OBJ에 관한 연재 게시물 이제 8회차 마지막편까지 왔습니다. 이번 회차에서는 Type 0에 해당되는 Triangulated 유형에 관하여 알아보겠습니다. 이 유형은 XYZ 3차원 공간상에 흩어져 있는 다수의 포인트들 즉 꼭지점(Vertex)들을 적절하게 연결하여 폴리곤을 생성하는 경우에 해당됩니다. 그리고 각 꼭지점의 XYZ 좌표만 존재할 뿐 이 점들이 구체적으로 어떻게 연결될 것인가에 해당되는 연결성(Connectivity)에 대한 사전 정보는 전혀 없는 경우입니다. 따라서 주어진 꼭지점들을 어떻게 “적절하게 연결”할 것인가에 대해서는 별도의 계산이 필요한데 이 때 삼각법(Triangulation)이라는 기법이 적용됩니다. 그러면 예제를 보기 위하여 다음과 같이 12개의 꼭지점들을 가정하고 X, Y, Z 좌표값들을 MESH_OBJ 명령에 입력 인수로 투입해봅시다. 그 과정은 다음과 같습니다.
xv = [0.8,3.0,1.5,0.1,1.0,2.3,1.8,3.1,5.8,6.9,5.4,8.7]
yv = [9.5,9.8,7.7,6.5,5.7,6.0,2.6,0.2,3.3,5.8,7.2,9.0]
zv = 0.8*FINDGEN(12)
arr = TRANSPOSE([[xv], [yv], [zv]])
MESH_OBJ, 0, vertices, polygons, arr
여기서 MESH_OBJ 명령에서는 Type에 해당되는 0이라는 값을 첫번째 인수로 주는 것 외에도 입력 인수 arr이 사용되고 있습니다. 그런데 P로 시작하는 명칭의 키워드들은 전혀 사용되고 있지 않은데, 실제로 Type 0의 경우는 키워드들은 전혀 지원되지 않고 오직 arr과 같은 좌표값 배열만 인수로 사용됩니다. 그리고 명령이 실행된 후 그 결과를 vertices, polygons로 돌려받게 됩니다. Type 0에서 정의되는 폴리곤은 삼각법에 의하여 모든 꼭지점들을 가장 적절하게 연결한 형태로 자동 생성됩니다. 결국 MESH_OBJ 명령을 실행하여 새로 입수되는 중요한 결과는 꼭지점들 사이의 적절한 연결성 정보에 해당되는 polygons가 됩니다. 이러한 "적절한 연결성"은 삼각법(Triangulation)이라는 기법에 의하여 산출되는데, 간단하게 얘기한다면 서로 가장 인접한 세 점들을 삼각형으로 이어주면서 이러한 여러 삼각형들이 전체적인 폴리곤을 구성하게되는 방식이라고 보면 됩니다.
일단 12개의 꼭지점들을 살펴보면 이들의 X, Y, Z 좌표값들은 각각 xv, yv, zv로 정의되어 있습니다. 이들의 분포 위치는 대략 X, Y, Z 방향으로 0~10의 범위를 갖습니다. 일단 먼저 이 꼭지점들의 위치 분포를 보는 것이 좋을 것 같아서 다음과 같이 PLOT3D 함수를 사용하여 가시화해봅시다.
win = WINDOW(DIMENSIONS=[600, 600], /NO_TOOLBAR)
p = PLOT3D(xv, yv, zv, AXIS_STYLE=2, ASPECT_Z=1, $
XRANGE=[0, 10], YRANGE=[0, 10], ZRANGE=[0, 10], $
SYM_OBJECT=ORB(), SYM_COLOR='crimson', SYM_SIZE=1.5, $
LINESTYLE=6, CLIP=0, /CURRENT)
이 과정에 의한 표출 결과는 다음 그림과 같습니다.
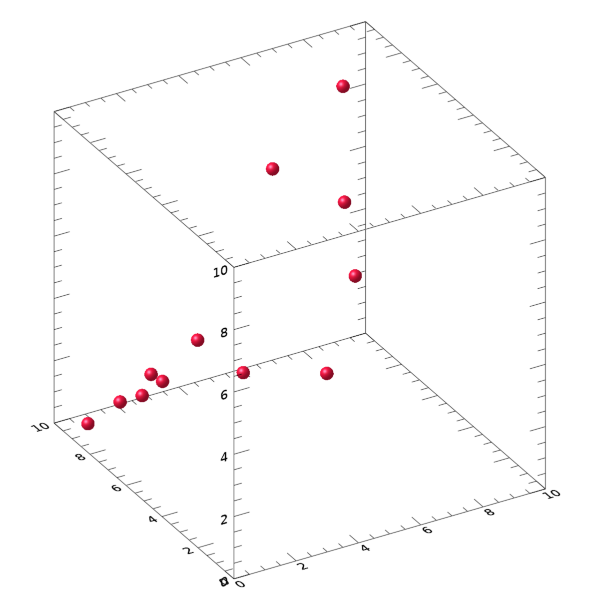
이와 같이 12개의 꼭지점들이 XYZ 공간상에 분포해 있는데, MESH_OBJ 명령을 사용하여 이 꼭지점들을 삼각법에 의하여 연결하고 그 연결성(Connectivity) 정보를 돌려받고자 하는 것입니다. 삼각법을 적용하면 가장 인점한 세 개의 꼭지점을 연결하게 되는데, 이러한 연결이 12개의 모든 꼭지점들에 대하여 적용되어야 합니다. 따라서 연결성 정보는 꽤 복잡해지게 됩니다. 앞서 MESH_OBJ 명령을 실행하여 얻은 polygons가 바로 그 결과입니다. 그러면 이 결과를 이용하여 꼭지점들이 모두 연결된 폴리곤을 표출해봅시다. 앞서 꼭지점들만 표출했던 과정을 다음과 같이 수정하면 됩니다.
win = WINDOW(DIMENSIONS=[600, 600], /NO_TOOLBAR)
p = PLOT3D(xv, yv, zv, ASPECT_Z=1, $
XRANGE=[0, 10], YRANGE=[0, 10], ZRANGE=[0, 10], $
/NODATA, /CURRENT)
pol = POLYGON(xv, yv, zv, CONNECTIVITY=polygons, $
COLOR='black', FILL_COLOR='green', CLIP=0, /DATA)
여기서는 PLOT3D 함수는 XYZ축으로 정의되는 3차원 공간만 표출하고 /NODATA 키워드를 사용하여 꼭지점들이 표시되지는 않도록 하였습니다. 그리고 이어서 POLYGON 함수를 사용함으로써 이 공간 내에 폴리곤의 형태가 표출되도록 하였습니다. 표출 결과는 다음 그림과 같습니다.

이 그림에서는 꼭지점들 사이를 연결하는 선들이 검은색으로 표시되어 있기 때문에, 앞서 MESH_OBJ 명령으로 얻은 연결성 정보가 어떤 방식으로 반영되어 있는지를 눈으로 쉽게 볼 수 있습니다. 결국 다수의 꼭지점들에 대한 좌표 정보만 주어지고 연결성 정보는 전혀 주어지지 않은 경우라면, MESH_OBJ 명령을 사용하여 적절한 연결성을 계산할 수 있고 결국 그 결과를 폴리곤의 형태로 표출할 수 있게 됩니다.
* 물론 만약에 꼭지점 좌표들 뿐 아니라 연결성에 관한 정보까지도 모두 확보된 경우라면, 굳이 여기서와 같이 MESH_OBJ가 동원될 필요도 없이 그냥 막바로 POLYGON 함수에 그 정보들을 바로 투입하면 됩니다.
그러면 지금까지 8회에 걸쳐 이어져온 MESH_OBJ에 관한 연재 게시물은 여기서 모두 마무리하도록 하겠습니다.
'IDL > New Graphics' 카테고리의 다른 글
| 서피스(Surface) 그림의 이동 (0) | 2023.03.02 |
|---|---|
| IDL에서 표(Table) 그리기(?) (0) | 2022.12.27 |
| 기호(Symbol)의 크기 설정 (0) | 2022.12.06 |
| MESH_OBJ 명령을 이용한 폴리곤 생성 방법 [7] (1) | 2022.10.05 |
| MESH_OBJ 명령을 이용한 폴리곤 생성 방법 [6] (0) | 2022.08.22 |