지난 회차에 이어서 오늘은 Type 2에 해당되는 Polar 유형에 관하여 알아보겠습니다. Polar 유형은 말 그대로 극좌표 기반 즉 각도(angle)와 반경(radius) 기반의 좌표로 정의된 꼭지점들로 구성된 폴리곤에 해당됩니다. 따라서 그 특성에 맞는 입력 정보들을 제공해주어야 하는데, 예제를 보면 다음과 같습니다.
p1 = 30*!DTOR
p2 = 270*!DTOR
p3 = 2
p4 = 6
arr = REPLICATE(4, 10, 5)
MESH_OBJ, 2, vertices, polygons, arr, $
P1=p1, P2=p2, P3=p3, P4=p4
여기서 MESH_OBJ 명령에서는 Type에 해당되는 2라는 값을 첫번째 인수로 주는 것 외에도 다양한 입력 인수 및 키워드들이 사용되고 있습니다. 전반적으로는 p1, p2, p3, p4, arr을 각각 정의하여 입력 인수로 투입하였고 그 결과를 vertices, polygons로 돌려받게 됩니다. Type 2에서 정의되는 극좌표형 폴리곤은 기본적으로는 중심이 (0, 0)이고 일정한 반경 및 각도 범위를 갖는 부채꼴 또는 고리 모양의 형태를 띄게 됩니다. 먼저 p3, p4는 시작 반경과 끝 반경입니다. 그리고 p1, p2는 시작 각도와 끝 각도인데 반드시 라디안(radian) 단위로 명시해야 하기 때문에 위와 같이 !DTOR을 곱해주었습니다. 그리고 arr은 격자들의 구조에 맞춰서 꼭지점들의 Z 방향 높이 값들로 구성된 2차원 배열입니다. 여기서는 4라는 높이 값들이 10x5의 격자 형태로 구성되었습니다. 그리고 반경의 범위가 2~6이 되고 각도 범위가 30도~270가 되도록 하였습니다.
이제 이렇게 정의된 폴리곤의 모습을 보기 위하여 다음과 같이 XYZ 축으로 구성된 3차원 공간을 정의하고 그 안에 폴리곤이 표출되도록 해봅시다. 이를 위하여 NG(New Graphics) 체계의 POLYGON 함수를 사용하게 되며, 앞서 MESH_OBJ 명령을 실행하여 얻은 결과물들인 vertices 및 polygons를 활용하게 됩니다. 그 과정은 다음과 같습니다.
xv = REFORM(vertices[0, *])
yv = REFORM(vertices[1, *])
zv = REFORM(vertices[2, *])
n = 20
x = RANDOMU(seed, n)*10
y = RANDOMU(seed, n)*10
z = RANDOMU(seed, n)*10
win = WINDOW(DIMENSIONS=[600, 600], /NO_TOOLBAR)
p = PLOT3D(x, y, z, ASPECT_Z=1, $
XRANGE=[0, 10], YRANGE=[0, 10], ZRANGE=[0, 10], $
/NODATA, /CURRENT)
pol = POLYGON(xv, yv, zv, CONNECTIVITY=polygons, $
COLOR='black', FILL_COLOR='green', CLIP=0, /DATA)
지금까지의 과정을 실행해보면 표출 결과는 다음 그림과 같습니다.

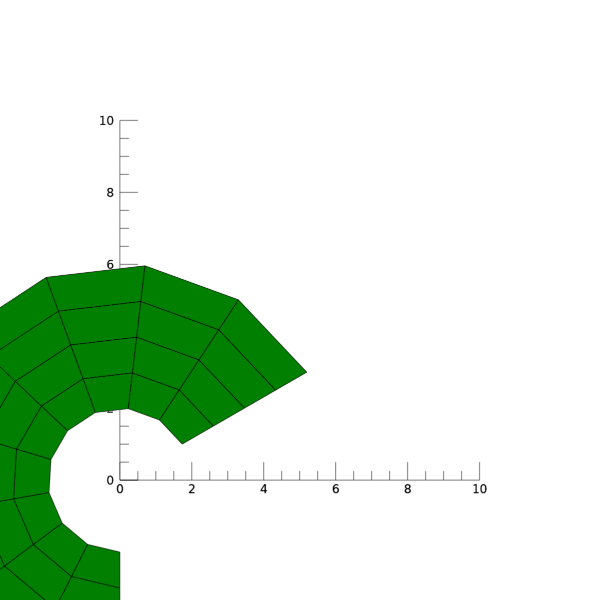
이와 같이 마치 끊어진 고리 모양과 같은 결과를 얻게 됩니다. 여기서 첫번째 그림은 그냥 바로 표출했을 때의 모습이고 두번째 그림은 동일한 대상을 마치 위에서 XY 평면을 내려다본 것과 같은 느낌으로 본 모습입니다. 그래서 두번째 그림을 보면 앞서 MESH_OBJ 명령에 부여했던 입력 정보들에 따른 기하학적 특성을 쉽게 확인할 수 있습니다. 다만 두번째 그림에서는 폴리곤 자체가 너무 왼쪽 하단에 위치하는 바람에 그 모습이 잘려 나가게 되긴 합니다. 그러면 이 결과를 바탕으로 하여 이번에는 입력 정보들을 다음과 같이 약간 변화시켜서 다른 결과를 얻어봅시다.
p1 = 0*!DTOR
p2 = 360*!DTOR
p3 = 0
p4 = 4
arr = REPLICATE(4, 36, 10)
MESH_OBJ, 2, vertices, polygons, arr, $
P1=p1, P2=p2, P3=p3, P4=p4
xv = REFORM(vertices[0, *])+5
yv = REFORM(vertices[1, *])+5
zv = REFORM(vertices[2, *])
이와 같이 입력정보들을 구성하면 마치 원형 디스크와 같은 모습의 폴리곤을 얻을 수 있습니다. 그리고 xv와 yv에 대하여 각각 5를 더함으로써 중심의 XY 좌표가 (0, 0)이 아닌 (5, 5)가 되도록 해보았습니다. 또한 격자 구조는 36x10이 되도록 하였습니다. 이러한 변화들을 반영하여 표출 과정까지 다시 실행해보면 그 모습은 다음 그림과 같습니다.
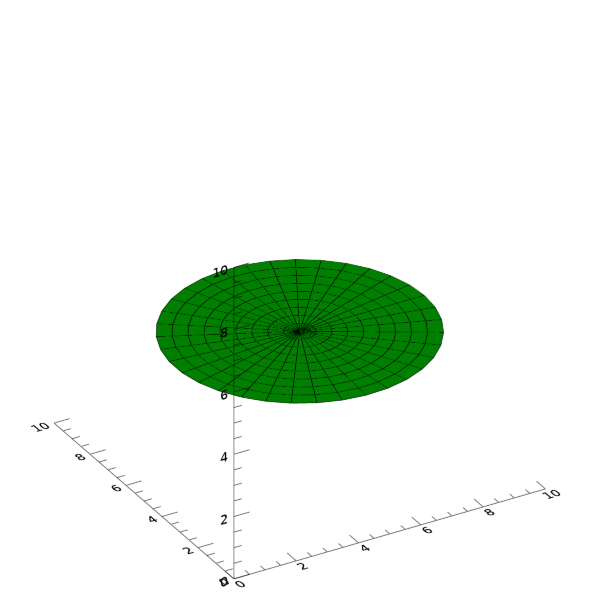
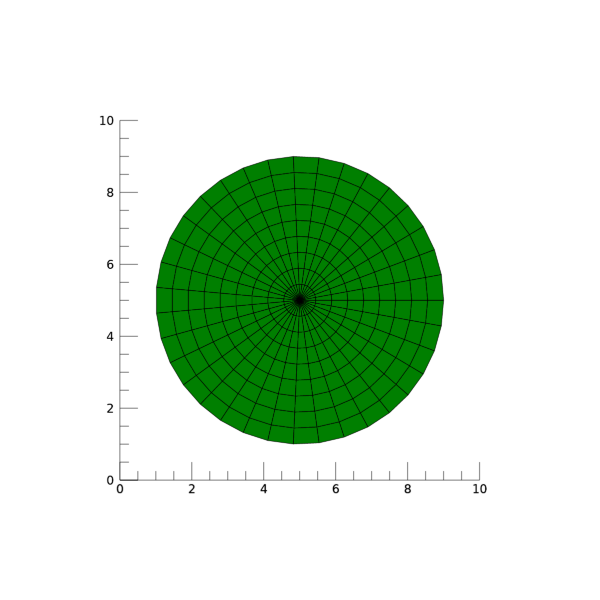
이와 같이 원형 디스크에 가까운 형태의 폴리곤을 얻었고 그 중심 좌표는 XY 평면상에서 (5, 5)가 됩니다. 만약 격자들의 개수를 더 늘려서 개별 격자의 크기를 줄인 촘촘한 형태로 바꾸게 되면 상당히 매끈한 원형 디스크의 형태를 갖는 폴리곤을 얻을 수 있게 됩니다. 예를 들면 다음과 같은 방식입니다.
arr = REPLICATE(4, 360, 10)
즉 이렇게 arr만 변경하고 전체 과정을 다시 실행해보면 결과는 다음과 같습니다.

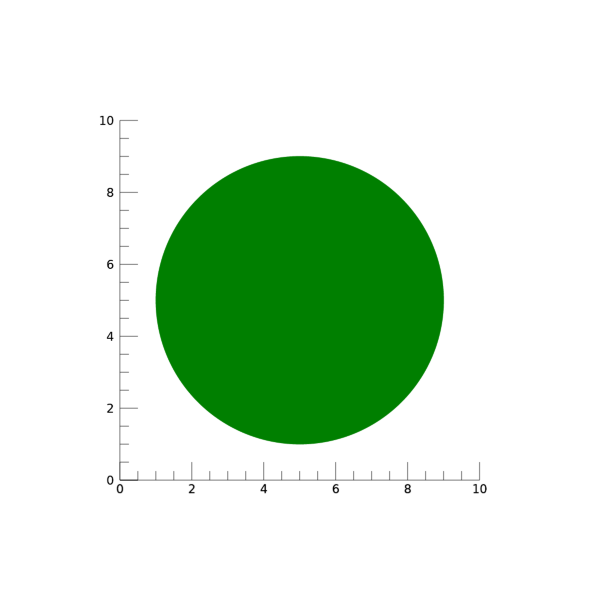
여기서는 격자선들이 굳이 보이지 않아도 될 것 같아서 POLYGON 함수에서 COLOR 속성을 ‘green’으로 처리하였음을 밝혀둡니다. 그리고 만약 여기서 P1, P2를 맨 처음과 같이 30도 및 270도로 정의하면 원형의 일부 각도 부위가 잘려진 형태의 폴리곤을 얻을 수도 있을 것입니다.
p1 = 30*!DTOR
p2 = 270*!DTOR

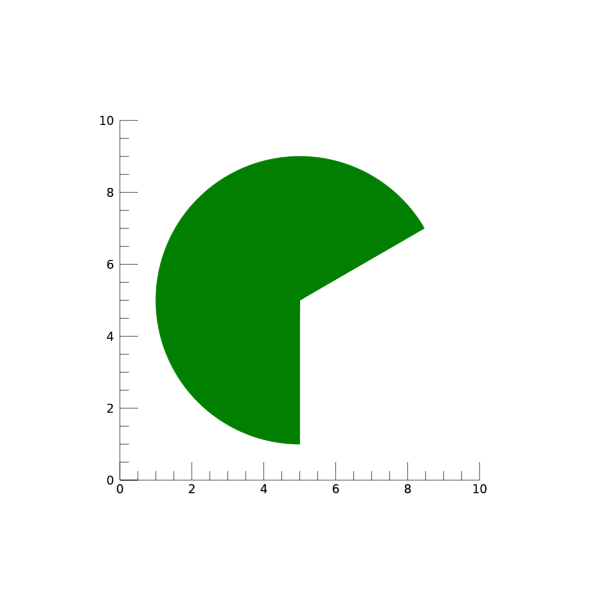
지금까지 살펴본 바와 같이 MESH_OBJ 명령에서 Type을 2로 설정하면 극좌표 기반으로 시작 각도와 끝 각도 그리고 시작 반경과 끝 반경을 조절하여 고리 형태, 원형 디스크, 부채꼴 등과 같은 다양한 형태의 폴리곤들을 비교적 쉽게 생성할 수 있게 됩니다. 이제 다음 회차에서는 Type 5 Extrusion 유형에 관하여 알아보도록 하겠습니다.
'IDL > New Graphics' 카테고리의 다른 글
| TEXT 함수 소개 (0) | 2022.07.26 |
|---|---|
| MESH_OBJ 명령을 이용한 폴리곤 생성 방법 [4] (0) | 2022.07.19 |
| MESH_OBJ 명령을 이용한 폴리곤 생성 방법 [2] (0) | 2022.07.06 |
| MESH_OBJ 명령을 이용한 폴리곤 생성 방법 [1] (0) | 2022.07.04 |
| SetData 메서드의 활용 예제 [2] (0) | 2022.06.30 |