우리가 데이터 분석 작업을 하는데 있어서 다수의 값들로 구성된 데이터에 대하여 값의 범위를 구간별로 나누어 각 구간별 빈도수를 확인해야 하는 경우가 많습니다. IDL에서는 HISTOGRAM 및 HIST_2D 함수가 그러한 역할을 합니다. 두 함수는 구간이 1차원적이냐 2차원적이냐의 차이라고 보면 되는데요. 오늘부터 2회에 걸쳐서 HISTOGRAM 및 HIST_2D 함수의 사용법 및 관련 예제들을 차례로 소개해보고자 합니다. 오늘은 먼저 HISTOGRAM 함수부터 살펴보겠습니다.
사실 HISTOGRAM 함수는 제가 이 블로그에 올린 여러 게시물들에서 활용된 바 있습니다. 다만 HISTOGRAM 함수 자체에 충실하게 소개했던 적은 의외로 없었기 때문에 이번이 좋은 기회인 것 같습니다. 일단 예제로 사용할 가상의 데이터를 먼저 생성해봅시다.
data = RANDOMU(seed, 10000, /NORMAL)*10+150
HELP, data
PRINT, MIN(data), MAX(data)
여기서는 RANDOMU 함수를 /NORMAL 키워드와 함께 사용하여 대략 정규 분포(Normal Distribution)을 하는 10000개의 값들로 구성된 배열을 생성하였습니다. 난수 발생 기능을 사용하기 때문에 제가 얻은 데이터와 여러분이 얻는 데이터는 당연히 똑같지는 않을 것입니다. 제 경우는 데이터의 최소값 및 최대값이 대략 110 및 186으로 산출되었습니다. 아마 여러분이 얻을 데이터도 대략 100~200 정도의 범위 내에서 값들이 존재할 것입니다.
이제 그 다음은 HISTOGRAM 함수를 바로 사용하여 데이터 값들의 범위 구간별 빈도수 즉 분포(Distribution)의 결과를 얻어야 합니다. IDL 도움말에서 HISTOGRAM 함수에 관한 내용을 찾아보면 자세한 설명이 소개되어 있겠지만, 제가 주로 권장하는 사용 방식은 다음과 같습니다.
bsz = 10
hist = HISTOGRAM(data, MIN=100, MAX=200-bsz, BINSIZE=bsz, LOCATIONS=xloc)
이와 같이 HISTOGRAM 함수에는 대상 배열이 필수 인수로서 명시되어야 하며 나머지는 키워드들입니다. 여기서 사용된 키워드들은 MIN, MAX, BINSIZE, LOCATIONS 등인데요. 일단 bsz라는 변수의 값을 10으로 정의해놓았는데, 이 값은 빈도 분포를 집계할 때 사용될 세부 구간의 크기(Bin Size)입니다. 그런데 구간을 정의할 때에는 세부 구간의 크기 뿐 아니라 전체 구간의 시작값과 끝값도 명확하게 정의해두는 것이 좋습니다. 여기서는 전체 구간의 시작값과 끝값을 MIN, MAX 키워드로 설정하였고 세부 구간의 크기를 BINSIZE 키워드로 설정하였습니다. 따라서 위와 같이 처리하면 구간들은 다음과 같이 정의됩니다.
100~110
110~120
120~130
..........
180~190
190~200
이와 같이 총 10개의 구간들로 정의됩니다. 그런데 위의 내용에서 MAX 키워드에 부여된 값을 보면 그냥 200이 아니라 200-bsz로 되어 있습니다. 굳이 이렇게 한 이유는 마지막 구간이 190~200이 되도록 하기 위함입니다. 만약에 MAX 키워드의 값을 그냥 200으로 할 경우에는 마지막 구간이 200~210이 됩니다. 즉 MAX 키워드의 값은 마지막 구간의 시작값으로 간주된다는 특성을 감안하였다고 보시면 됩니다. 그리고 BINSIZE 키워드는 말 그대로 세부 구간의 크기이기 때문에 그 값을 bsz로 설정하였습니다. 그리고 LOCATIONS 키워드가 있는데요. 이 키워드는 값을 내가 부여하기 위한 것이 아니라 이 키워드를 통하여 뭔가를 돌려받기 위하여 사용됩니다. 여기서는 xloc이라는 이름으로 뭔가를 돌려받았는데 다음과 같은 방법으로 xloc의 실체를 확인해봅시다.
HELP, xloc
PRINT, xloc
출력된 내용을 보면 다음과 같습니다.
XLOC FLOAT = Array[10]
100.000 110.000 120.000 130.000 140.000 150.000 160.000 170.000 180.000 190.000
이와 같이 각 세부 구간의 시작값들로 구성된 배열임을 확인할 수 있습니다. 이것은 나중에 표출 과정에서 유용하게 사용될 수 있기 때문에 가급적이면 LOCATIONS 키워드를 사용하여 이러한 정보를 얻어두는 것이 좋습니다. HISTOGRAM 함수에는 기타 다른 키워드들도 지원되지만 제 생각에는 위와 같은 방식으로 핵심적인 키워드들을 사용하는 것이 가장 좋을 것 같습니다. 자 그러면 HISTOGRAM 함수를 사용하여 구간별 빈도 분포 결과를 hist라는 이름으로 얻었으므로 이 결과에 대한 정보를 다음과 같이 출력해봅시다.
HELP, hist
PRINT, hist
출력된 결과는 대략 다음과 같을 것입니다. 다시 말씀드리지만 제 결과와 여러분의 결과는 똑같지는 않을 것입니다.
HIST LONG = Array[10]
0 6 200 1353 3512 3364 1324 232 9 0
이 내용을 보면 hist는 각 구간별 빈도수를 집계한 결과임을 확인할 수 있습니다. 그런데 결과를 좀 더 보기 좋게 하려면 다음과 같이 반복형 구문을 이용하여 각 구간별 시작값, 끝값, 빈도수를 함께 출력하는 것이 좋을 것 같습니다.
FOR j = 0, N_ELEMENTS(hist)-1 DO $
PRINT, xloc[j], xloc[j]+bsz, hist[j]
실제로 출력된 내용은 다음과 같습니다. 아무래도 이렇게 보는 것이 훨씬 더 일목요연할 것입니다.
100.000 110.000 0
110.000 120.000 6
120.000 130.000 200
130.000 140.000 1353
140.000 150.000 3512
150.000 160.000 3364
160.000 170.000 1324
170.000 180.000 232
180.000 190.000 9
190.000 200.000 0
이 결과를 보면 가운데 구간들의 빈도수가 가장자리 구간들에 비하여 훨씬 높은 것을 알 수 있습니다. 애초에 정규분포 기반의 데이터를 생성하여 얻은 결과이기 때문에 대략 이런 모습으로 나올 것입니다. 어쨌든 HISTOGRAM 함수를 사용하여 데이터의 구간별 빈도 분포 결과를 얻는 작업은 이러한 방식으로 처리하면 됩니다. 물론 아직 일이 다 끝난 것은 아닙니다. 이 결과를 그래픽으로 표출하는 과정이 남아있기 때문입니다. 사실 HISTOGRAM 함수가 그 이름 때문에 마치 그래픽 표출까지도 해줄 것처럼 보일 수도 있겠지만, 이 함수는 분포의 결과를 산출하는 역할일 뿐 그래픽 표출까지 직접 해주지는 않는다는 것을 유념해야 합니다. 이를 위해서는 그래픽 기능을 추가적으로 사용해야만 하는데, 가장 전형적이고 편리한 방법은 NG 체계의 BARPLOT 함수를 사용하여 막대 그래프와 같은 형태로 표출하는 것입니다. 그러면 바로 이어서 이 방법을 사용하여 표출 과정까지 진행해봅시다. 그 과정은 다음과 같습니다.
win = WINDOW(DIMENSIONS=[600, 500], /NO_TOOLBAR)
p = BARPLOT(xloc+bsz/2., hist, FILL_COLOR='orange', $
XTICKINTERVAL=bsz, XMINOR=0, XTICKLEN=0, $
XTITLE='Data Value', YTITLE='Count', $
MARGIN=0.1, FONT_SIZE=10, /CURRENT)
여기서는 BARPLOT 함수가 사용된 방식에 주목해야 하는데요. 가장 먼저 X 및 Y에 해당되는 필수 인수들은 각각 xloc+bsz/2. 및 hist가 사용되었습니다. 일단 X 인수에서 xloc이 사용된 것은 각 구간의 위치에 막대가 표시되도록 하기 위한 것이고, Y인수로 사용된 hist는 당연히 구간별 빈도값에 해당됩니다. 다만 xloc이 아닌 xloc+bsz/2.라는 형태로 사용한 것은 나름의 이유가 있는데 이것은 나중에 다시 살펴보기로 하겠습니다. 그리고 XTICKINTERVAL 속성의 값을 bsz로 설정하였는데 이것은 X축에서 구간별 눈금 간격이 그만큼이 되도록 하기 위한 것입니다. 그리고 XMINOR 속성을 0으로 설정하여 마이너 눈금들이 아예 보이지 않도록 하였고, XTICKLEN 속성을 0으로 설정하여 X축의 눈금선이 아예 보이지않도록 설정하였습니다. 왜냐하면 X축의 눈금들이 막대들을 보는데 있어서 약간 방해가 된다고 판단했기 때문입니다. 일단 표출 결과 그림부터 보면 다음과 같습니다.
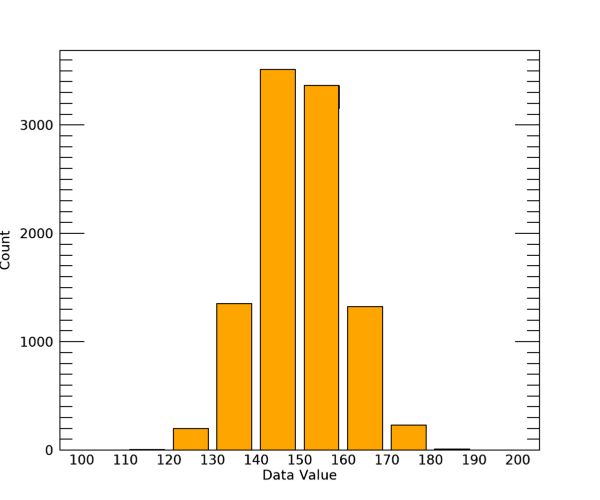
물론 표출의 방식은 프로그래머의 판단에 따라 얼마든지 조정할 수 있겠지만 저는 이렇게 하는 것이 깔끔하지 않을까 생각을 해보았습니다. 그리고 앞서 잠시 보류해두었던 xloc+bsz/2.에 관한 얘기로 돌아가보면, 만약 다음과 같이 앞서 BARPLOT 함수가 사용된 부분에서 X 인수를 그냥 xloc으로 처리할 경우에 어떻게 되는지 살펴봅시다.
p = BARPLOT(xloc, hist, FILL_COLOR='orange', $
XTICKINTERVAL=bsz, XMINOR=0, XTICKLEN=0, $
XTITLE='Data Value', YTITLE='Count', $
MARGIN=0.1, FONT_SIZE=10, /CURRENT)
이 경우의 결과 그림은 다음과 같습니다.

이와 같이 구간 경계값 눈금에 막대의 중심이 오게 됩니다. 그래서 빈도수가 정확히 어느쪽(왼쪽 또는 오른쪽) 구간에 대한 것인지 헷갈리기 쉽습니다. 따라서 맨 처음에 했던 것처럼 X 인수를 xloc+bsz/2.로 처리하면 막대가 구간의 경계값 사이에 정확히 위치하게 되기 때문에, 구간별 빈도수를 보여준다는 본래의 취지에 좀 더 부합되지 않을까 생각을 합니다.
그리고 HISTOGRAM 함수로 얻은 결과에 대하여 다음과 같이 TOTAL 함수와 /CUMULATIVE 키워드를 함께 적용하면 말 그대로 누적형(Cumulative) 빈도 분포 결과를 얻을 수도 있습니다. 즉 특정 구간에 대한 빈도수가 이전 구간들의 빈도수 총합이 되는 방식입니다.
chist = TOTAL(hist, /CUMULATIVE)
이렇게 얻은 결과인 chist를 역시 BARPLOT 함수를 사용하는 유사한 방식으로 표출하는 과정은 다음과 같습니다.
win = WINDOW(DIMENSIONS=[600, 500], /NO_TOOLBAR)
p = BARPLOT(xloc+bsz/2., chist, FILL_COLOR='green', $
XTICKINTERVAL=bsz, XMINOR=0, XTICKLEN=0, $
XTITLE='Data Value', YTITLE='Count', $
MARGIN=0.1, FONT_SIZE=10, /CURRENT)
그리고 그 결과는 다음 그림과 같습니다.
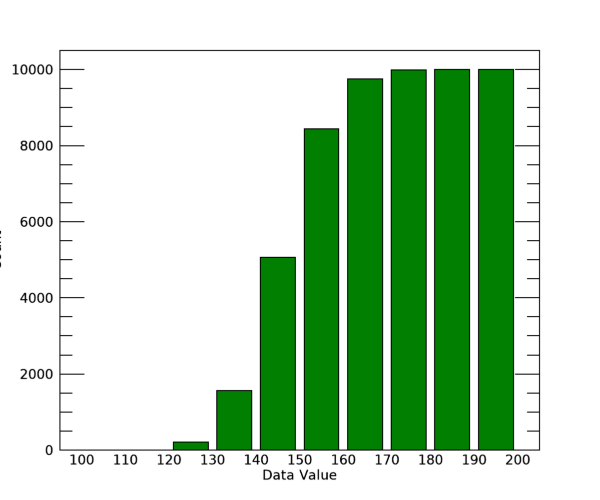
그리고 앞서 bsz라는 변수의 값을 10으로 정의하여 세부 구간의 크기가 10이 되도록 하였는데, 이를 다른 값으로 변경하면 세부 구간의 크기가 달라진 결과를 얻을 수 있으므로 직접 테스트해보시기 바랍니다. 지금까지 데이터의 값 구간별 분포를 얻고 그 결과를 표출하기 위하여 HISTOGRAM, BARPLOT 등의 함수들을 사용하는 방법 및 예제를 살펴보았습니다. 아마도 이 정도면 충분히 정리가 되었다고 봅니다. 다음 회차에서는 HIST_2D 함수를 사용하여 2차원적 구간별 분포를 얻고 그 결과를 표출하는 방법을 살펴보기로 하겠습니다.
'IDL > Programming' 카테고리의 다른 글
| FILE_INFO 함수의 활용법 (0) | 2022.03.02 |
|---|---|
| HISTOGRAM 및 HIST_2D 함수의 활용 [2] (0) | 2022.01.06 |
| 벡터(Vector)의 각도에 대한 정의 및 관련 이슈 (0) | 2021.12.03 |
| FILE_SEARCH 함수에 관하여 (0) | 2021.07.14 |
| SAVE 명령 및 IDL_SAVEFILE 클래스의 사용에 관하여 [2] (0) | 2021.03.15 |