지난 회 게시물에서는 격자화된 벡터장 데이터가 있을 때, VECTOR 함수를 사용하여 이를 가시화하고, 이러한 벡터장 내에서 특정 위치의 입자가 이동하게 될 궤적을 PARTICLE_TRACE 프로시저를 사용하여 추적하는 방법에 관하여 소개하였습니다. 이 예제에서는 벡터장 내에서 단 하나의 입자를 가정하여 그 이동 경로를 추적해보았는데요. 원래 PARTICLE_TRACE 프로시저를 사용하면 하나 또는 다수의 입자들을 가정하여 추적하는 것도 가능합니다. 예를 들어서 서로 다른 위치에 있는 3개의 입자들을 가정하여 이들의 이동 궤적을 한꺼번에 추적해봅시다. 이를 위하여 지난 게시물에서 작성했던 예제코드의 내용을 거의 그대로 가져오겠습니다. 벡터장 데이터를 읽고, 바탕 지도를 표출하고, 그 위에 벡터장을 중첩 표출하는 과정은 다음과 같이 그대로입니다.
file = FILEPATH('globalwinds.dat', SUBDIR=['examples','data'])
RESTORE, file
win = WINDOW(DIMENSIONS=[800, 480], /NO_TOOLBAR)
m = MAP('Geographic', LIMIT=limit, FILL_COLOR='light blue', $
MARGIN=0.05, /CURRENT)
mc = MAPCONTINENTS(FILL_COLOR='gold')
m.MapGrid.LABEL_POSITION = 0
m.MapGrid.GRID_LONGITUDE = 30
m.MapGrid.LINESTYLE = 2
m.MapGrid.HORIZON_LINESTYLE = 0
vec = VECTOR(u, v, x, y, AXIS_STYLE=2, ARROW_THICK=3, $
HEAD_SIZE=0.5, /HEAD_PROPORTIONAL, LENGTH_SCALE=0.5, $
COLOR='green', /OVERPLOT)
여기까지의 과정에 대한 자세한 설명은 이미 지난 게시물에서 했으므로 여기서는 생략합니다. 그러면 여기서 3개의 입자들의 초기 위치에 대한 인덱스 좌표들을 다음과 같이 정의합니다.
seeds = [[92, 32], [42, 28], [109, 45]]
즉 여기서 정의된 3개 입자들의 인덱스 좌표는 각각 [92, 32], [42, 28], [109, 45]이며 이들을 seeds라는 하나의 배열로 합쳐놓았습니다. 나중에 PARTICLE_TRACE 프로시저에서는 이 seeds를 그대로 input 자료로 사용하게 됩니다. 일단은 3개 입자들 각각의 인덱스 좌표에 대한 실제 경도/위도 좌표를 확인해보고, 이 지점들을 지도상에 파란색 원형 심볼로 표시하고자 합니다. 이 과정은 다음과 같습니다.
FOR j = 0, 2 DO BEGIN
x_ind0 = seeds[0, j]
y_ind0 = seeds[1, j]
PRINT, 'lon/lat of the starting point :', x[x_ind0], y[y_ind0]
sym = SYMBOL(x[x_ind0], y[y_ind0], 'circle', $
SYM_COLOR='blue', /SYM_FILLED, SYM_SIZE=1.5, /DATA)
ENDFOR
PRINT 명령에 의하여 출력된 내용은 다음과 같습니다.
lon/lat of the starting point : 78.7500 1.00000
lon/lat of the starting point : -61.8750 -10.2500
lon/lat of the starting point : 126.562 37.5625
그리고 3개 입자들의 시작 위치가 표시된 그림은 다음과 같습니다.

이제 3개 입자들의 이동 궤적을 추적하기 위하여 PARTICLE_TRACE 프로시저를 사용합니다. 사용법은 이미 지난 게시물에서 언급했던 것과 거의 같습니다. 단지 오늘은 input 인수로 seeds가 들어간다는 차이만 있을 뿐입니다.
data = FLTARR(2, 128, 64)
data[0, *, *] = u
data[1, *, *] = v
n_iter = 30
PARTICLE_TRACE, data, seeds, verts, conn, $
MAX_ITERATIONS=n_iter
HELP, verts, conn
일단 여기서는 결과로 얻어진 verts, conn에 관하여 출력된 정보를 주목해볼 필요가 있습니다. 출력된 내용은 다음과 같습니다.
VERTS FLOAT = Array[2, 90]
CONN LONG64 = Array[93]
이와 같이 verts는 [2, 90]의 구조를 갖는 2차원 배열로서 총 90개의 점들에 대한 X, Y 인덱스 좌표값들이 수록되었는데요. 90개인 이유는 3개의 입자들 각각 30회에 걸쳐서 추적한 좌표들을 모두 한꺼번에 담고 있기 때문(3x30=90)입니다. 그리고 conn의 경우는 93개의 값들로 구성된 1차원 배열인데, 이것은 3개의 각 입자에 대한 연결성(Connectivity) 정보에 해당되는 값들이 각각 31개씩이기 때문(3x31=93)입니다. 특히 3개 입자들의 이동 궤적을 POLYLINE 함수를 이용하여 표출하는데 있어서 이 conn 배열은 반드시 필요합니다. 그러면 바로 이어서 이 작업을 진행해봅시다. 그 과정은 다음과 같습니다.
x_inds = REFORM(verts[0, *])
y_inds = REFORM(verts[1, *])
line = POLYLINE(x[x_inds], y[y_inds], CONNECTIVITY=conn, $
THICK=3, COLOR='red', /DATA)
그리고 표출 결과는 다음과 같습니다.

이와 같이 PARTICLE_TRACE 프로시저에서는 다수의 N개의 입자들에 대해서도 초기 위치를 정의한 다음 각각의 이동 궤적을 추적할 수 있습니다. 그런데 이와 같은 다수의 입자들에 대한 추적을 좀 더 간편하고 깔끔하게 할 수 있도록 해주는 기능이 있는데요. 바로 STREAMLINE 함수입니다. 이 기능을 사용하면 마치 입자 추적의 대상이 될 입자들이 격자형으로 골고루 분포한 상태에서 일제히 추적을 수행한 것과 같은 결과를 얻을 수 있습니다. 이 예제를 보여드리기 위해서는 아예 그림을 처음부터 다시 그려야하기 때문에, 우선 바탕 지도 표출부터 다음과 같이 먼저 진행합니다.
win = WINDOW(DIMENSIONS=[800, 480], /NO_TOOLBAR)
m = MAP('Geographic', LIMIT=limit, FILL_COLOR='light blue', $
MARGIN=0.05, /CURRENT)
mc = MAPCONTINENTS(FILL_COLOR='gold');, /HIRES)
m.MapGrid.LABEL_POSITION = 0
m.MapGrid.GRID_LONGITUDE = 30
m.MapGrid.LINESTYLE = 2
m.MapGrid.HORIZON_LINESTYLE = 0
그 다음에는 바로 이어서 STREAMLINE 함수를 다음과 같이 사용해봅시다.
stream = STREAMLINE(u, v, x, y, COLOR='crimson', THICK=2, /OVERPLOT, $
STREAMLINE_STEPSIZE=0.1, STREAMLINE_NSTEPS=30, $
ARROW_OFFSET=1, ARROW_SIZE=0.4, ARROW_THICK=3)
이와 같이 STREAM 함수 역시 VECTOR 함수와 마찬가지로 u, v, x, y가 필수인자들로 사용됩니다. 물론 여기서는 필수인자들 외에도 여러가지 부가적인 속성들도 사용하였는데요. 일단 표출 결과를 보면 다음과 같습니다.

이 그림을 보면 아마 STREAMLINE 함수의 기능이 어떤 것인지에 대한 감을 잡을 수 있을 것입니다. 실제로는 기본적으로 전체 영역 내에서 25x25의 격자 형태로 총 625개의 입자들을 뿌려놓고 이 모든 입자들에 대한 추적 결과를 한꺼번에 보여준 것입니다. 그리고 위의 내용에서는 STREAMLINE_STEPSIZE, STREAMLINE_NSTEPS와 같은 속성들이 사용되었는데, 입자 추적의 단계별 크기 및 단계 갯수에 해당됩니다. 이 속성들의 값을 적절히 설정하면 추적 경로의 길이를 조절할 수 있습니다. 디폴트 상태일 경우에는 추적 경로가 너무 길어져서 시각적으로 가독성이 안좋아지기 때문에 위와 같이 0.1과 30이란 값으로 설정한 것입니다. 그 외에 ARROW_로 시작되는 이름의 속성들은 화살표의 표시와 관련된 것들입니다. 그리고 추적 대상 입자들의 격자형 분포의 형태를 조정하는 것도 가능합니다. 이것은 다음과 같이 STREAMLINE 함수 내에서X_STREAMPARTICLES 및 Y_STREAMPARTICLES 속성을 추가적으로 사용하여 조정하면 됩니다.
stream = STREAMLINE(u, v, x, y, COLOR='crimson', THICK=2, /OVERPLOT, $
STREAMLINE_STEPSIZE=0.1, STREAMLINE_NSTEPS=30, $
X_STREAMPARTICLES=10, Y_STREAMPARTICLES=10, $
ARROW_OFFSET=1, ARROW_SIZE=0.4, ARROW_THICK=3)
여기서는 10x10의 형태로 입자들의 총 갯수를 100개로 대폭 줄여보았습니다. 그 결과는 다음 그림과 같습니다.

이와 같이 처음에 비하여 훨씬 더 듬성듬성하게 입자들이 분포한 상태에서 추적이 진행된 것을 볼 수 있습니다. 제 생각에는 다음과 같이 20x20 정도가 되도록 하는 것이 적당할 것 같습니다.
stream = STREAMLINE(u, v, x, y, COLOR='crimson', THICK=2, /OVERPLOT, $
STREAMLINE_STEPSIZE=0.1, STREAMLINE_NSTEPS=30, $
X_STREAMPARTICLES=20, Y_STREAMPARTICLES=20, $
ARROW_OFFSET=1, ARROW_SIZE=0.4, ARROW_THICK=3)
그 결과는 다음 그림과 같습니다.
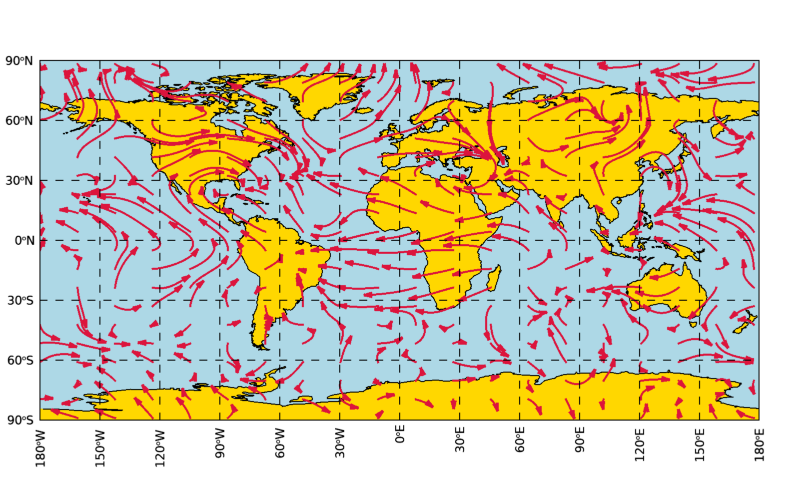
앞서 벡터장 내에서 3개의 입자들을 가정하여 추적을 했었는데요. 이번에는 이와 같이 STREAMLINE 함수에 의한 표출이 되어 있는 상태에서 이 3개의 입자들에 대한 추적 결과도 중첩하여 표출해봅시다. 이를 위하여 앞서 이미 작업했던 내용을 다음과 같이 그대로 다시 적어서 실행하면 됩니다.
seeds = [[92, 32], [42, 28], [109, 45]]
FOR j = 0, 2 DO BEGIN
x_ind0 = seeds[0, j]
y_ind0 = seeds[1, j]
PRINT, 'lon/lat of the starting point :', x[x_ind0], y[y_ind0]
sym = SYMBOL(x[x_ind0], y[y_ind0], 'circle', $
SYM_COLOR='blue', /SYM_FILLED, SYM_SIZE=1.5, /DATA)
ENDFOR
data = FLTARR(2, 128, 64)
data[0, *, *] = u
data[1, *, *] = v
n_iter = 30
PARTICLE_TRACE, data, seeds, verts, conn, $
MAX_ITERATIONS=n_iter, INTEGRATION=0
HELP, verts, conn
x_inds = REFORM(verts[0, *])
y_inds = REFORM(verts[1, *])
line = POLYLINE(x[x_inds], y[y_inds], CONNECTIVITY=conn, $
THICK=3, COLOR='blue', /DATA)
그러면 그 결과는 다음과 같습니다.
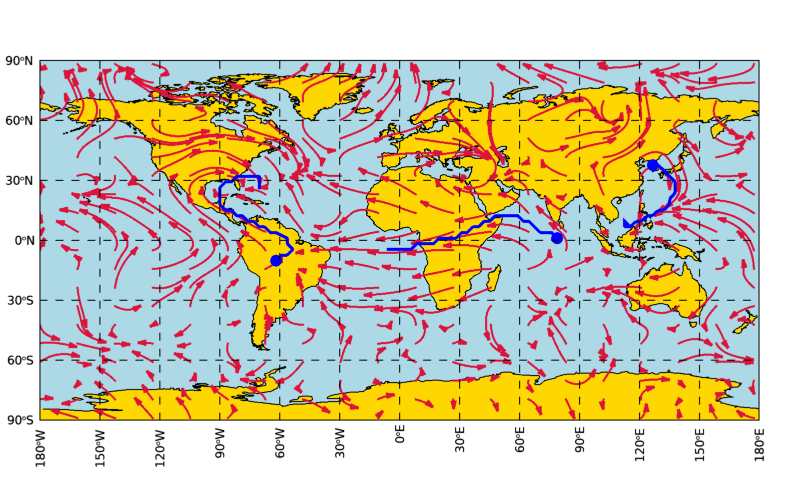
이 그림을 보면 3개의 입자들이 이동한 궤적을 주변의 Streamline들과 비교해볼 수 있는데요. 입자들이 이동한 궤적이 주변의 유체 흐름과 충분히 유사하다는 것을 확인할 수 있습니다.
정리해보면 PARTICLE_TRACE 프로시저를 이용한 입자 추적은 하나 또는 다수의 입자들을 대상으로 추적을 하는 것이고, STREAMLINE 함수를 이용한 입자 추적은 입자들을 아예 격자 형태로 다량으로 뿌려놓고 추적을 하는 것이라고 보면 됩니다. 어떤 방식을 사용하든간에 근본적인 취지는 유체의 흐름을 나타내는 벡터장 데이터가 있을 때 그 안에서 입자들이 흐름을 타고 이동하는 궤적을 추적하는 것입니다. 따라서 이러한 목적의 작업이 필요한 경우에는, 지금까지 2회에 걸쳐 소개해드린 내용을 한번 참조해보시면 좋을 것 같습니다.
'IDL > New Graphics' 카테고리의 다른 글
| NG 체계에서 Select 메서드의 활용 (0) | 2021.03.23 |
|---|---|
| 색상을 채운 플롯(Filled Plot)의 표출 [3] (0) | 2021.03.03 |
| 벡터장(Vector Field)과 입자 추적(Particle Tracing) [1] (0) | 2021.01.18 |
| 버블 플롯(Bubble Plot)에서 컬러테이블 적용 방법 (0) | 2020.12.11 |
| BUBBLEPLOT 함수 소개 (0) | 2020.12.09 |